Suddividiamo il tempo totale in cinque intervalli, a, b, c, d, e. Δt = 1 secondo.
Lo spazio percorso nell’intervallo di tempo sarà uguale alla velocità media (Va,Vb,Vc,Vd,Ve) moltiplicata l’intervallo di tempo Δt. Nel primo secondo lo spazio percorso è Sa= Va*Δt.
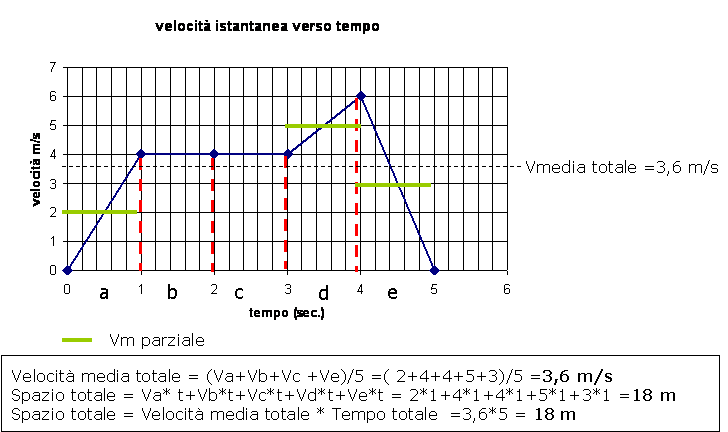
In pratica il valore medio della velocità è la superficie sottostante dell’andamento velocità istantanea (quella che leggiamo su un tachimetro, istante per istante) verso l’intervallo di tempo considerato (Matematicamente è un integrale definito della funzione V (t)). Volutamente ho fatto un esempio che rappresenta figure geometriche di cui tutti siamo capaci di calcolare l’area (triangoli, rettangoli e trapezio)
L’area del triangolo è base per altezza/ 2 , nel primo secondo abbiamo (1*4)/2= 2 quindi abbiamo una velocità media Va= 2 m/s che rappresento con la linea verde. Nel secondo intervallo, b , abbiamo un rettangolo (base per altezza) quindi 1*4 =4. La velocità media Vb = 4 m/s che coincide con quella istantanea poiché è costante (moto uniforme). Stesso discorso per il terzo intervallo, Vc= 4m/s
Dal terzo al quarto secondo abbiamo un trapezio di cui area è (base maggiore + base minore) per altezza /2= ((6+4) *1)/2= 5 quindi Vc= 5 m/s. Nel quarto intervallo abbiamo un triangolo, quindi Ve = 3 m/s.
La media aritmetica dei cinque valori di velocità medie parziali è di 3,6 m/s che corrisponde alla velocità media totale su tutto il percorso. Avrei potuto dividere il tempo totale in infiniti intervalli 1 ma, la velocità media sarebbe stata sempre di 3,6 m/s.
Attenzione a non considerare la velocità media come la media tra la velocità finale, Vf, e iniziale, Vi. Nel nostro caso la velocità iniziale è uguale a zero come pure la velocità finale, quindi (Vf+Vi)/2 = 0 e non 3,6 m/sec.
La velocità media moltiplicata per tutta la base di cinque secondi dà esattamente l’area totale sottostante all’andamento del grafico che non è altro che la somma delle superfici delle figure geometriche che lo compongono (triangolo + rettangolo + trapezio + triangolo). Oppure l’area totale rappresenta anche la distanza totale percorsa (spazio totale) da cui ricaviamo la velocità media. Nel nostro esempio 18 metri.
Nella realtà è impensabile avere solo velocità e accelerazioni costanti. La velocità istante per istante varia in continuazione. La conoscenza della velocità media non ci dice nulla quale velocità massima abbiamo raggiunto. Nel nostro semplice esempio la velocità dell’oggetto raggiunge tutti i valori da 0 a 6 m/s (21,6 km/h).
A cosa è servito conoscere la velocità media? A ricavare lo spazio percorso senza sapere nulla del valore istantaneo della velocità.
Nel caso dell’automobile ciò non serve poiché il contachilometri esegue l’integrale della velocità istantanea nel tempo e ci indica lo spazio percorso.
Spesso in diverse branche della fisica si ha a che fare con grandezze che si muovono nel tempo come delle velocità. Esempio la corrente elettrica, il flusso di calore, la portata d’acqua e ovviamente la velocità di un oggetto. Conoscendo il valore medio della corrente elettrica, del flusso di calore, della portata di un fiume, della velocità di un corpo, possiamo ricavare rispettivamente le grandezze derivate che sono: la quantità di carica elettrica, il volume dell’acqua che scorre, la quantità di calore che si scambia, lo spazio percorso. La carica elettrica è l’integrale della corrente elettrica come lo è lo spazio verso la velocità 2.
Nulla cambierebbe nel ragionamento se nel nostro esempio di grafico mettessimo al posto della velocità la corrente elettrica. Il grafico rappresenterebbe l’andamento della corrente istantanea verso il tempo cui corrisponderebbe un valore medio di corrente di 3,6 ampere.
Note
1) Nel nostro semplice esempio non serve a nulla aumentare gli intervalli poiché siamo stati in grado di risolverlo senza la conoscenza dell’analisi matematica.
Nei casi (In realtà quasi sempre) che la superficie sottostante all’andamento velocità verso tempo non corrisponda alla sommatoria di semplici figure geometriche dobbiamo ricorrere all’analisi matematica.
Per ottenere il valore esatto della distanza percorsa per poi ricavare la velocità media dobbiamo aumentare il numero, n, d’intervalli temporali Δt a un valore grandissimo. Tanto grande in modo che Δt sia talmente piccolo tale che nell’intervallo corrispondente a ΔS le variazioni di velocità istantanea siano irrilevanti rispetto al valore medio. In soldoni è come se tutti i tipi di moti esistenti fossero sempre dei moto uniformi (velocità costante) all’interno di Δt. In fondo tutto si può considerare fermo e costante in un tempo infinitesimo.
Per chi conosce l’analisi matematica, si tratta di fare un limite per n che tende all’infinito:
.gif)
Sugli integrali definiti si legga:
2) Ci tengo ricordare ai giovani studenti che la prima rivoluzione scientifica (1687) permise, grazie alle acute e meticolose osservazioni dei movimenti di oggetti fatte da Brahe, Keplero e Galileo, a Newton e Leibniz di darci, oltre alla teoria gravitazionale, il più potente mezzo di analisi matematica usato in tutte le discipline scientifiche presenti e future (Integrali, derivate e limiti).
Le leggi del moto furono una grande rivoluzione scientifica per i secoli successivi. Dovete pensare che, nei primi tempi della fisica moderna, i fenomeni del moto erano separati dai fenomeni del calore, del suono, dei fluidi, della luce e della corrente elettrica. Secoli dopo alcuni scienziati, che avevano studiato le leggi di Newton e l’analisi matematica (memoria) grazie all’aggiunta di fantasia e creatività, scoprirono che molti di questi fenomeni diversi tra loro erano in realtà la stessa cosa. Intere sezioni della fisica furono unificate. Calore, corrente elettrica, fluidi, onde meccaniche, segnali telegrafici, tutto fu comprensibile come moto di atomi, cariche ecc. Fu quindi possibile usare le stesse leggi del moto e la stessa analisi matematica. La cosa sorprendente è che la teoria della gravitazione, che fu l’origine di tutto, non è ancora spiegabile (in data di oggi) in termini di altri fenomeni. Resta separata da tutte le altre teorie. La scoperta che leggi del moto non sono valide alle distanze atomiche (1929) fu un’altra rivoluzione scientifica.
.gif)