Anche se questi due problemi sembrano semplici, in realtà non lo sono affatto e le soluzioni complete non sono esprimibili in termini di una semplice formula che contempli le classiche operazioni disponibili su una calcolatrice. Abbiamo a disposizione due strade:
- adottare alcune semplificazioni che portino ad un risultato approssimato ma semplice,
- costruire una tabella dei dati sperimentali disponibili ed utilizzare una procedura di interpolazione per ottenere la temperatura di ebollizione per una altitudine generica.
Te(z) ~ 373 K / ( 1 + 8.8 10-6 z )
dove Te(z) è la temperatura assoluta di ebollizione dell’acqua e z è l’altitudine espressa in metri. Per ottenere la temperatura in gradi Celsius è sufficiente sottrarre 273 K dalla temperatura assoluta.
Questa formula implica inoltre che, almeno a basse quote, per ogni aumento unitario di z la temperatura di ebollizione scende di 3.3 millesimi di grado.
Dipendenza della pressione dall’altitudine.
Trascuriamo ogni considerazione legata alle condizioni meteorologiche ed immaginiamo di avere un’atmosfera immobile e a temperatura costante. Trattiamo inoltre l’aria come gas perfetto, assumiamo quindi che la sua equazione di stato sia data da:
p = n R Tatm
dove p è la pressione, n è il numero di moli per unità di volume, Tatm la temperatura ed R la costante universale dei gas uguale a 8,3144 J/(mol*K). Per i nostri scopi introduciamo la variabile z per indicare l’altitudine. Vogliamo determinare la funzione p(z) e, poiché la temperatura è supposta costante, dall’equazione di stato vediamo che n(z) è proporzionale a p(z). Per avere una situazione di equilibrio meccanico ogni strato di aria deve essere sostenuto dagli strati sottostanti, quindi, per uno strato sottile di spessore dz all’altezza z dobbiamo avere
g d n dz = p(z) – p(z+dz) = – dp
dove g è l’accelerazione terrestre e d è la massa di una mole di gas. Possiamo riscrivere l’equazione nel seguente modo
g d n = – dp/dz
ed utilizzando l’equazione di stato possiamo ricavare
g d p = – R Tatm dp/dz
Integrando questa equazione differenziale otteniamo
p(z) = C exp( – z g d/R Tatm )
dove C è una costante arbitraria.
Sapendo che alla quota z=0 la pressione è p0 e la densità n0 possiamo scrivere
p(z) = p0 exp( – z g d/R Tatm )
n(z) = n0 exp( – z g d/R Tatm )
La pressione diminuisce quindi in modo esponenziale con l’altezza e la lunghezza di dimezzamento di questo decadimento (il valore di z per qui la pressione è metà di quella a livello zero) è
z1/2 = log(2) R Tatm/(g d)
che per l’azoto a temperatura ambiente vale approssimativamente 6000 metri.
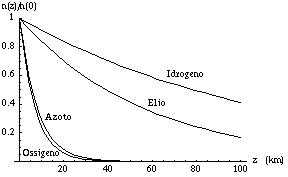
È ovvio che questo risultato è fortemente condizionato dalle assunzioni iniziali, in particolare dall’ipotesi di temperatura costante che è fortemente irrealistica. Si possono anche studiare dei modelli con assunzioni diverse, ad esempio quella adiabatica analizzata in una precedente risposta.
Comunque, per andare più a fondo è necessario ipotizzare un modello di trasporto del calore, includere una dinamica, distinguere fra le diverse componenti dell’atmosfera e così via, ma le cose si complicano notevolmente.
Anche per questo problema sono necessarie delle semplificazioni. Innanzitutto quello a cui siamo interessati è la cosiddetta tensione di vapore che è definita nel seguente modo. Fissata una temperatura T consideriamo una certa quantità di acqua allo stato liquido sottoposta ad una forte pressione in un volume chiuso. Immaginiamo ora di aumentare progressivamente il volume. Ad un certo punto l’acqua inizierà a bollire e all’interno del contenitore si formerà una certa quantità di vapore. La pressione alla quale inizia l’ebollizione viene chiamata pressione di vapore che indichiamo con pv(T). Continuando ad aumentare il volume, il liquido si trasforma progressivamente in gas e la pressione rimane costante. Ad un certo punto tutto il liquido diventa gas e la pressione riprende a scendere con l’aumentare del volume1.
Per ogni temperatura il valore della pressione di vapore determina la condizione alla quale si verifica l’ebollizione. Questo significa che, fissata una pressione p, la temperatura di ebollizione è determinata della condizione pv(T) = p.
Una strada molto semplice per stimare pv(T) consiste nel partire dal secondo principio della termodinamica e dedurre la seguente equazione detta di Clausius-Clayperon2:
L/[ T ( Vg – Vl ) ] = dpv(T)/dT
dove L è il calore necessario per vaporizzare una mole di acqua, T è la temperatura e Vg e Vl sono i volumi occupati rispettivamente da una mole di liquido e una mole di gas. Ovviamente L, Vg e Vl dipendono dalla temperatura ma, siccome per i nostri scopi siamo interessati solo all’interavallo da 0 a 100 gradi, possiamo assumere che Vl in questo intervallo sia trascurabile rispetto a Vg. Inoltre possiamo approssimare L(T) ad una costante nonostante questo sia molto meno giustificabile. Trattando inoltre il vapore come un gas perfetto possiamo scrivere
Vg = R T/pv(T)
e quindi semplificare l’equazione di Clausius-Clayperon a
L pv(T)/( R T2) = dpv(T)/dt
Separando le variabili possiamo integrare e ottenere
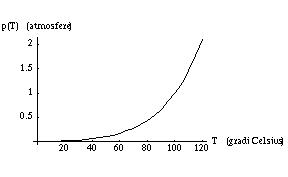
pv(T) = C exp( -L/R T )
dove nel nostro caso la costante C può essere fissata dal fatto che a 100 gradi la tensione di vapore è di una atmosfera.
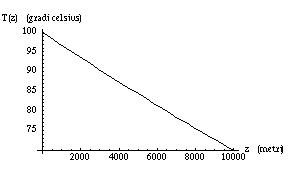
Temperatura di ebollizione Te(z) dell’acqua in funzione dell’altitudine.
A questo punto possiamo mettere assieme i due risultati:
p(z) = p0 exp( – z g d/R Tatm )
pv(T) = C exp( – L/R T )
Uguagliando le due pressioni otteniamo
Te(z) = L/(Cost. + z g d/Tatm )
Possiamo utilizzare L ~ 4.5 104 J/mole, g ~ 10 m/s, d ~ 2.9 10-2, Tatm ~ 273 K e fissare la costante richiedendo Te(z=0) = 373 K. Misurando z in metri si trova
Te(z) ~ 373 K / (1 + 8.8 10-6 z )
che è il risultato precedentemente anticipato e discusso.
Referenze:
1Una rappresentazione grafica di questo processo si può trovare a questo link.
2Si veda per esempio The Feynman Lectures on Physics, volume I, 45-3.