 Facendo
Facendo
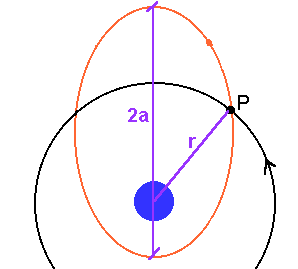
riferimento alla figura a lato, si chiede se nel punto P di incontro tra
le due traiettorie, le velocità dei due corpi orbitanti sono uguali.
Per qualsiasi corpo orbitante in un campo gravitazionale, esiste una quantità
invariante: l’energia meccanica totale, data dall’equazione
![]()
G
al solito è la costante di gravitazione universale, M è la massa
della Terra, m è la massa del corpo in orbita, a è il semiasse
maggiore dell’orbita (se l’orbita è circolare a coincide con il
raggio r).
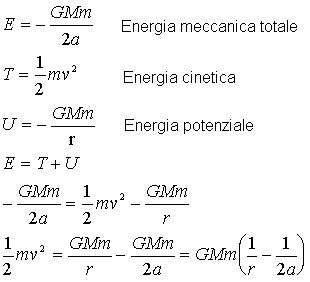
Dato che
l’energia meccanica totale è la somma di energia potenziale U (che
dipende dalla posizione del corpo rispetto alla Terra) e di energia
cinetica T (che dipende dalla velocità del corpo rispetto alla Terra),
allora possiamo scrivere l’espressione dell’energia totale come di seguito:
Da cui ricaviamo
la velocità :
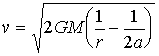
dove r
è la distanza dalla Terra del corpo in orbita.
Ora osserviamo che nel punto P i due corpi hanno la stessa distanza dalla
Terra e dunque nell’equazione precedente riferita al punto P, l’unico
parametro che può variare è il semiasse a.
Giungiamo
dunque alla conclusione che i due corpi hanno velocità uguali nel punto
di incontro soltanto se i semiassi delle rispettive orbite sono uguali.
Se invece a1 < a2 allora v1 < v2.
N.B.
quando si dice “velocità uguali” si intende che il loro modulo
è uguale, la direzione in generale è diversa !