Effettivamente
la prima legge di Keplero è la più semplice da enunciare
ma al contempo la più difficile da ricavare. Newton infatti la
dimostrò nell’opera Principia Matemathica Philosophiae naturalis
dando un contributo fondamentale non solo all’astronomia, ma anche all’analisi
matematica, poiché per la dimostrazione mise a punto il calcolo
differenziale (che egli però raffigurava geometricamente chiamandolo
metodo delle flussioni).
Trovare
un modo semplice per ricavare l’equazione dell’orbita di un pianeta partendo
dall’espressione della forza, dell’energia e del momento angolare è
impresa ardua. Meglio dire chiaramente che senza la soluzione di un’equazione
differenziale del primo ordine:
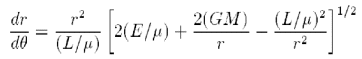
dove 
non
ci possiamo arrivare per mezzo di equazioni.
Tuttavia
è possibile lavorare in modo semi-intuitivo operando come fece
una delle menti più brillanti di questo secolo: il fisico teorico
Richard P. Feynman durante la lezione
che tenne alle matricole del California Institute of Tecnology il 13 marzo
1964.
La
brillante lezione sul moto dei pianeti intorno al sole sfrutta strumenti
matematici non più complessi della geometria piana. Negli appunti di Feynman
sono stati trovati evidenti riferimenti alla dimostrazione delle leggi
di Keplero, come quelli che Newton aveva riportato nei suoi “Principia
Mathematica”, ma come dice Feynman stesso, ad un certo punto della lezione
il procedimento della dimostrazione è del tutto originale.
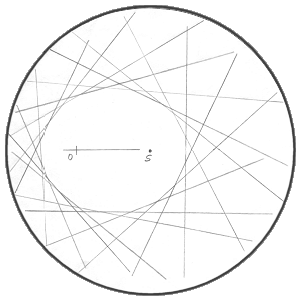
Infatti
la dimostrazione di Newton data nei Principia Mathematica è
difficile da seguire perché si appoggia su astruse proprietà
geometriche delle ellissi. Inoltre la dimostrazione parte dal moto ellittico
e giunge a dimostrare che la forza che lo determina è centrale
e dipende dall’inverso della distanza. Feynman invece parte dall’espressione
della forza centrale che dipende dall’inverso del quadrato della distanza,
dal fatto che l’orbita è un percorso chiuso con una distanza minima
ed una massima dal Sole, dalla seconda legge di Keplero che impone la
costanza delle velocità areolari, e giunge a dimostrare che l’orbita
risultante è una ellisse.
Tale
dimostrazione si trova nel libro in lingua italiana
Il
moto dei pianeti intorno al Sole
titolo originale: “Feynman’s Lost Lecture, The Motion of Planets Around
the Sun”
di D.L. Goodstein e J.R. Goodstein
Editore: Zanichelli – Collana: Le ellissi
Prezzo: £ 28.000
Oppure,
se si ha confidenza con la lingua inglese, la stessa
dimostrazione è reperibile in internet.
Consiglio di seguire tale dimostrazione avendo a disposizione un foglio
circolare di una ventina di centimetri di diametro. L’autore della pagina
web sopra riportata suggerisce di ripiegare il foglio per visualizzare
l’ellisse, ma io aggiungo di ripassare le pieghe con un tratto di matita
(come suggerisce il metodo originale di Feynman).