La risposta più semplice potrebbe essere questa: La Terra
quando si approssima al punto più vicino a Marte, si affianca al
pianeta, ma la sua velocità angolare è più elevata
perché impiega solo un anno per compere un giro, Marte invece ne
impiega 1,8 e dunque resta indietro mostrando un moto retrogrado. Dopo
il massimo avvicinamento Marte riprende il suo moto diretto.
Il modo più efficace per spiegare il fenomeno direi che è
rappresentato dall’applet java qui a fianco. Il punto verde non indica
un pianeta esterno, ma la direzione in cui è visto Marte dalla
Terra. Il cursore permette di modificare la velocità angolare
del pianeta esterno e dunque, in ottemperanza alla terza legge di Keplero,
la sua distanza dal Sole.
Per semplificare
la trattazione matematica, supporremo che le orbite della Terra e di Marte
siano circolari, Il periodo orbitale della Terra valga 1 anno e così
pure la distanza dal Sole sia di 1 unità astronomica. In questo
modello Marte orbita alla distanza di 1,6 unità astronomiche, il
periodo orbitale, determinato dalla terza legge di Keplero, verrà
arrotondato a 2 anni.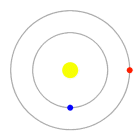
Supponiamo
che la situazione iniziale sia quella illustrata in figura: per descrivere
matematicamente l’evoluzione del sistema porremo
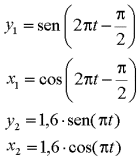
per trovare
la direzione della retta Terra-Marte, vale a dire dove è visto
Marte rispetto alla Terra, calcoliamo la pendenza della retta come (y2-y1)/(x2-x1)
e per ricavarne la direzione calcoliamo
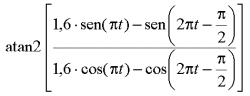
dove atan2
restituisce l’angolo di direzione della retta Terra-Marte.
Il grafico
seguente mostra la direzione in cui punta la linea Terra-Marte nel periodo
di due anni. Il senso diretto è verso l’alto, quello retrogrado
in basso. E’ evidente che intorno alla metà del primo anno la direzione
si inverte e poi torna a muoversi in senso diretto.
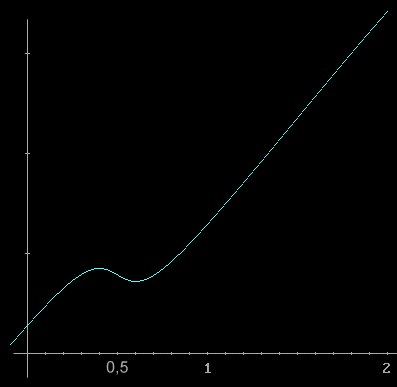
Cosa succede
se variamo la velocità angolare (in altre parole, se consideriamo
pianeti più esterni o più vicini all’orbita terrestre) ?
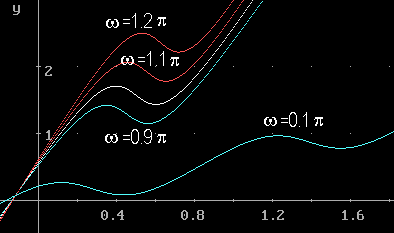
Il grafico seguente mostra la linea bianca corrispondente al valore di
omega=
, circondata da altre
linee con passo di 0,1. Per
valori di omega inferiori a
vediamo che le fasi retrograde si avvicinano sempre più, al di
sotto di un certo valore la traiettoria in realtà è un cappio
continuo, con una lenta deriva in senso diretto.
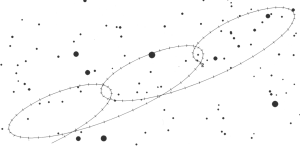
Ecco un
tracciato del percorso di Plutone, il pianeta più esterno del Sistema
solare. Il moto apparente nell’arco di quasi tre anni è proprio
una serie di cappi con una lenta deriva in senso diretto.
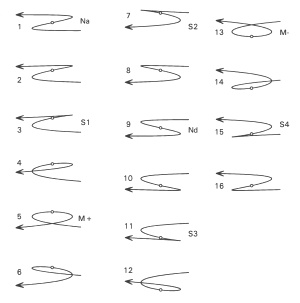In
realtà il cappio è solo una delle possibili configurazioni
per il moto retrogrado di Marte: la figura a fianco mostra alcune traiettorie
di Marte durante l’opposizione (figura tratta da Mathematical astronomy
morsels di Jean Meeus, Willmann-Bell Inc.)
Ciò che determina la forma della curva è la componente della
velocità di Marte perpendicolare all’eclittica. Tanto per fare
un esempio: se Marte si trova al nodo discendente della sua orbita, allora
si sta spostando velocemente verso latitudini eclittiche negative e dunque
la proiezione del cappio lungo la latitudine eclittica sarà discendente
(caso n°9), se invece si trova all’elongazione massima in latitudine
eclittica, allora durante il cappio sarà visto salire e poi scendere
(caso n°5). La componente “orizzontale” invece è
determinata dalla differenza tra la velocità angolare della Terra
e di Marte proiettata sul piano dell’eclittica.
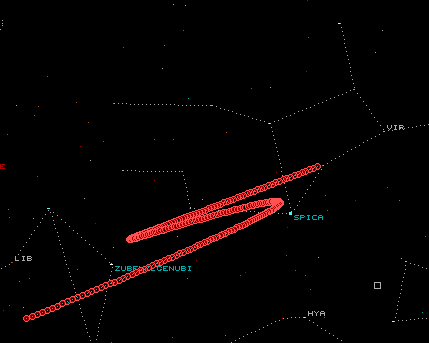
Il percorso
di Marte nei primi otto mesi del 1999.
grazie mille molto interesssante