Che cosa è la pietra celtica? Vorrei conoscere la teoria del sorprendente comportamento di questo oggetto e i dettagli per poterne fare una per dar sfogo alla mia passione di bricoleur. Una volta c’era una trottolina che nella sua rotazione, dopo un po’ si capovolgeva: c’è un’analogia?

Premessa

La trottolina cui fa riferimento il lettore è cosa diversa da quella che viene chiamata “pietra celtica“. Infatti, mentre quest’ultima, se fatta ruotare in un certo senso, inverte la rotazione, la trottolina citata dal lettore si comporta esattamente come egli ha scritto: avviata la rotazione, dopo un po’ si capovolge.

Sembra una trottola come tante, ma quando la facciamo ruotare abbiamo
la sorpresa di vederla capolvolgere su se stessa per continuare poi a
ruotare sul picciolo, cioè la punta che avevamo preso fra le dita per
darle la spinta.

Non e’ un trucco, ma il risultato di alcune leggi fisiche che operano durante il moto di questo oggetto!

Eccola qui la simpatica “antotrottola” che, dopo un po’ di rotazioni “normali”,
si capovolge continuando la sua rotazione posandosi sulla parte più stretta.

La pietra celtica

La trottola dispettosa, detta anche rattleback e pietra celtica,
è un bizzarro oggetto a forma di barchetta che presenta la peculiarità
che se messo in rotazione con un certo verso si comporta come una
trottola normale, mentre se messo in rotazione nel verso opposto
rallenta la rotazione beccheggiando fino a fermarsi, per poi mettersi
in rotazione nel verso opposto! Il comportamento non è di facile
analisi quantitativa, a causa delle grosse complicazioni. Per cui ci
limitiamo a darne una spiegazione qualitativa.

Ogni corpo esteso
possiede gli assi di inerzia, detti anche assi liberi di rotazione, che
sono quegli assi intorno a cui l’oggetto ruota liberamente se non è
sottoposto a momenti esterni. Se il corpo possiede delle simmetrie i
suoi assi sono infiniti perché tra essi ci saranno tutti gli assi di
simmetria del corpo: per esempio un cilindro omogeneo possiede come
assi di simmetria l’asse del cilindro e qualsiasi retta che passi per
il punto medio dell’asse del cilindro e gli sia perpendicolare. Se
tuttavia il corpo non gode di nessuna proprietà di simmetria, comunque
possiederà almeno tre assi di inerzia che si incontrano nel centro di
massa del corpo.

La trottola dispettosa è un oggetto che non
possiede proprietà di simmetria in quanto ha la forma di un
semiellissoide cui viene ulteriormente cancellata la simmetria per
riflessione con una distribuzione non omogenea della masse.

Quando
la trottola dispettosa viene messa in rotazione su un piano essa è
costretta a ruotare intorno ad un asse perpendicolare alla superificie
superiore, asse che però non coincide con alcun asse di rotazione. Per
tale motivo la trottola, oltre che ruotare, beccheggia oscillando.
Questi due movimenti combinati, insieme con la presenza di un attrito
sulla superficie cui è poggiata, provocano l’insorgere di un momento
che modifica il momento angolare del corpo fino a farne invertire la
rotazione. A causa della disomogeneità nella distribuzione della massa
del corpo, l’effetto si verifica solo per un verso di rotazione e non
per il verso opposto.

Due immagini della trottola dispettosa. Fa parte della categoria delle trottole speciali. Fu scoperta da alcuni archeologi e fu chiamata anche pietra celtica. Ha un verso di rotazione preferenziale:
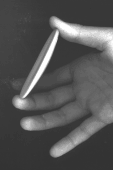
se fatta ruotare dalla parte “giusta”, essa mantiene il moto
normalmente, se, invece, la si fa ruotare “controsenso”, dopo poco l’oggetto
comincia ad oscillare sempre più stranamente e poi si ferma quasi e
riparte nell’altro senso.
Il suo comportamento è dovuto ad una non-simmetria nella forma,
che si può ottenere anche con una non simmetria nella distribuzione
dei pesi.

Bibliografia

Bondi,
Sir Hermann. F. R. S. “The Rigid Body Dynamics of Unidirectional Spin.”
Proceedings of the Royal Academy of London, A405, 1986, pp. 265-274.

Walgate, Robert. “Tops That Like To Spin One Way.” Nature, V. 323, 18 September, 1986,p.204.

Walker G. T. “On A Dynamical Top.” Lon: Quarterly Journal of Pure and Applied Mathematics, V. 28, 1896, pp. 175-184.

Walker,
Jearl. “The Amateur Scientist. The mysterious ‘rattleback’: a stone
that spins in one direction and then reverses.” Scientific American,
October, 1979, pp. 172-184.

Wheeler, Dr. Nicholas A. “Rattlebacks – How Do They Work?” Portland, Oregon: Reed College Department of Physics (no date).