Perché i numeri irrazionali non sono numerabili?

Iniziamo da una breve premessa teorica. Supponiamo di avere
due insiemi finiti A e B aventi, rispettivamente, m
e n elementi. È allora immediato rendersi conto che:

1. è possibile definire una funzione iniettiva da A a B
   se e soltanto se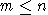
   ,
2. è possibile definire una funzione suriettiva da A a
   B se e soltanto se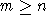
   ,
3. è possibile definire una funzione biiettiva (cioè, biunivoca)
   da A a B se e soltanto se m = n.

In particolare, nel caso degli insiemi finiti, l’esistenza
di una funzione iniettiva da A a B è equivalente
all’esistenza di una funzione suriettiva da B a A, e le
seguenti proposizioni sono equivalenti:

1. esistono una funzione suriettiva e una iniettiva da A a B,
2. esistono una funzione suriettiva e una iniettiva da B a A,
3. esistono due funzioni iniettive, una da da A a B e una
   da B a A,
4. esistono due funzioni suriettive, una da da A a B e
   una da B a A,
5. esiste una funzione biiettiva tra A e B,
6. A e B hanno lo stesso numero di elementi, cioè
   m = n.

Sotto ipotesi estremamente ragionevoli (ma di formulazione
e comprensione piuttosto complessa), è possibile dimostrare che
l’equivalenza tra l’esistenza di una funzione suriettiva da A a
B e l’esistenza di una funzione iniettiva da B a A
non necessita dell’ipotesi che A e B siano finiti. L’importantissimo
teorema di Schroeder-Cantor-Bernstein afferma inoltre che le prime cinque
proposizioni viste qui sopra sono equivalenti qualsiasi siano gli insiemi
A e B.

      Questi risultati teorici
portano a dare le seguenti definizioni, estensione naturale del concetto
di “numero di elementi” di un insieme:

1. si dice che l’insieme A ha cardinalità minore
   dell’insieme B (nel senso “lato”, corrispondente cioè
   al concetto di “minore o uguale” tra numeri) se è possibile definire
   una funzione iniettiva da A a B o, equivalentemente, se
   è possibile definire una funzione suriettiva da B a A;
2. si dice che gli insiemi A e B hanno la stessa cardinalità
   se è possibile definire una funzione biiettiva tra A e
   B o, equivalentemente, se vale una qualsiasi delle proposizioni
   1-4 viste sopra.

Inoltre, si dirà che l’insieme A ha cardinalità
strettamente minore dell’insieme B se la cardinalità
di A è minore della cardinalità di B ma non
uguale. Un insieme avente la stessa cardinalità dell’insieme dei
numeri naturali si dice numerabile; la cardinalità numerabile
è la più piccola cardinalità infinita.

      Arrivando ora alla
domanda, iniziamo a osservare che la cardinalità dell’insieme dei
numeri reali è uguale alla cardinalità dell’intervallo aperto
(0, 1): per convincersene, basta osservare che (per esempio) la funzione

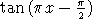
è una funzione biiettiva tra l’intervallo (0, 1) e l’insieme
di tutti i numeri reali. Per dimostrare che i numeri reali non sono numerabili,
allora basta dimostrare che l’intervallo (0, 1) non è numerabile.
Per far questo, possiamo usare il metodo della diagonalizzazione,
con cui Cantor per primo diede una risposta alla domanda di cui ci stiamo
occupando.

      Supponiamo, per assurdo,
che l’intervallo (0, 1) sia numerabile. Questo significa che è
in corrispondenza biunivoca con l’insieme dei numeri naturali, e quindi
che posso associare a ogni numero nell’intervallo (0, 1) uno e un
solo numero intero e scrivere (0, 1) = {x₁,
x₂, x₃, …} . Una volta eliminate
le notazioni “ambigue” decidendo di non usare “nove periodici” negli sviluppi
decimali (si veda la risposta a riguardo),
inoltre, l’intervallo (0, 1) è in corrispondenza biunivoca
con l’insieme degli sviluppi decimali del tipo 0,a₁a₂a₃… ,
per cui possiamo scrivere tutto l’intervallo (0, 1) in una
“tabella infinita” 

x 1	=	0,	a 1,1	a 1,2	a 1,3	a 1,4	…	a 1,n	…
x 2	=	0,	a 2,1	a 2,2	a 2,3	a 2,4	…	a 1,n	…
x 3	=	0,	a 3,1	a 3,2	a 3,3	a 3,4	…	a 1,n	…
			.	.	.
xm	=	0,	am,1	am,2	am,3	am,4	…	am,n	…

dove ogni riga rappresenta un numero dell’intervallo (0, 1)
insieme con tutto il suo sviluppo decimale (a_m,n
è la n-esima cifra dello sviluppo decimale del m-esimo
numero — nota che può eventualmente essere a_m,n = 0
da un certo n in poi, come per esempio in 1/2 = 0,50000…).
Ricordiamo che se l’intervallo (0, 1) fosse numerabile, allora tutti
i numeri dell’intervallo (0, 1) sarebbero contenuti in questa tabella.

      Costruiamo ora un numero
b=0,b₁b₂b₃…
scegliendo come n-esima cifra del suo sviluppo decimale un numero
b_n diverso da a_n,n,
da 0 e da 9. Dal momento che b è diverso da 0,000… = 0
e da 0,999… = 1, si ha che b appartiene all’intervallo
(0, 1). Ma b è diverso da ognuno dei numeri b_m,
perchè — per costruzione — ne differisce almeno per la m-esima
cifra decimale. Allora b non è compreso nella tabella appena
fatta, e quindi (per assurdo) siamo costretti a negare l’ipotesi che l’intervallo
(0, 1) fosse numerabile. Se ne deduce allora che l’insieme dei numeri
reali ha una cardinalità strettamente maggiore dell’insieme dei
numeri naturali, cioè che non è numerabile.