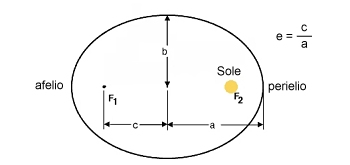
In molti libri di fisica e astronomia si legge che la distanza media di un pianeta dal Sole e’ pari al semiasse maggiore ‘a’ della sua orbita ellittica. Non capisco però in che senso va intesa la media: sul tempo? sull’angolo?

Effettivamente
molti testi, anche autorevoli, riportano l’affermazione errata secondo
la quale siccome nell’orbita ellittica il punto più vicino al Sole
(perielio) si trova alla distanza a(1-e) e il punto più
lontano dal Sole (afelio) si trova alla distanza a(1+e)
allora la distanza media del pianeta è la media delle distanze
appena menzionate dunque a.

Possiamo estendere questo ragionamento nel seguente modo, suggerito da Giancarlo Albricci.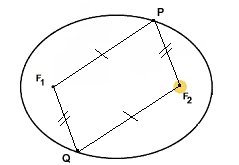
Sia P un punto qualsiasi dell’ellisse, F₂ il fuoco in cui sta il Sole, F₁ l’altro fuoco dell’ellisse.
Ora prendo un quarto punto Q sull’ellisse in questo modo:
1) se P e’ il perielio, Q e’ l’afelio e viceversa
2) negli altri casi Q il quarto vertice del parallelogramma F₁PF₂Q

Sia nel caso 1) che nel caso 2) abbiamo QF₁ = PF₂
Inoltre per le proprieta’ focali:
PF₁ + PF₂ = 2a

Dato che per ogni punto P trovo uno e un solo punto Q corrispondente posso
calcolare il valore medio della distanza dal Sole per le sole due posizioni
P e Q.

(PF₂ + QF₂) / 2 = (PF₁ + QF₁) /2 = 2a /2 = a

Ripeto lo stesso procedimento per tutte le infinite coppie P e Q e avro’
sempre che la media a due a due e’ uguale al semiasse maggiore a. Quindi
anche la media fatta considerando tutte le infinite coppie di posizioni
sull’ellisse e’ uguale al semiasse maggiore.

Tuttavia, una semplice riflessione porta ad osservare che un pianeta, in osservanza
alla seconda legge di Keplero, passa molto più tempo all’afelio
che non al perielio, dunque intuitivamente la “distanza media” è maggiore della media delle distanze massima e minima.

Occorre infatti
chiarire se si intende calcolare una media:

– sull’angolo, cioè dividendo l’angolo giro in tanti angoli uguali Dq e calcolando la media dei raggi vettori così spaziati;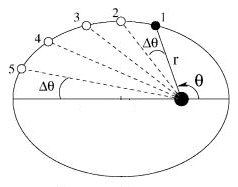
– sul tempo, cioè dividendo il periodo orbitale in tanti intervalli di tempo e calcolando la media dei raggi vettori dei diversi istanti di tempo.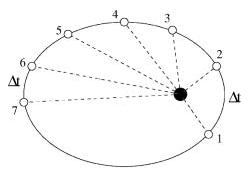

Il primo
metodo dà – dopo qualche calcolo –
cioè la distanza media calcolata in base all’angolo descritto dal
raggio vettore è tanto più piccola quanto maggiore è
l’eccentricità. Questo
tipo di media però non è di grande interesse per l’astronomo
perché l’angolo descritto dal pianeta non è una grandezza
direttamente misurabile, inoltre non dà informazioni di particolare
valenza scientifica.

Molto più
interessante è la media rispetto al tempo.
Per calcolarla si immagina, come abbiamo già detto, di descrivere
l’orbita come successione di tanti raggi vettori intervallati dallo stesso
tempo.
Dopo alcuni passaggi matematici si giunge al risultato
cioè la distanza media è tanto più elevata quanto
maggiore è l’eccentricità, proprio come suggeriva l’intuito.
Tracciamo il grafico della funzione d_m/a per
analizzare il rapporto tra la grandezza corretta e quella riportata dai
libri di testo.

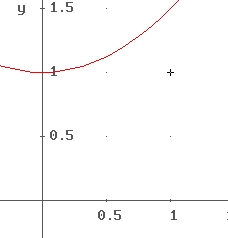Per
piccole eccentricità lo scostamento è contenuto. Nel sistema
solare il pianeta con orbita più eccentrica è Mercurio (e
= 0.2) in tal caso lo scostamento ammonta a circa il 2%.
Corpi celesti più particolari, come gli asteroidi, Plutone o le
comete hanno eccentricità che possono arrivare a 0,96 e l’errore
arriva dunque a sfiorare il 50% !

Dando un’occhiata
ai pianeti extrasolari recentemente scoperti, ci accorgiamo che hanno
un’orbita piuttosto eccentrica, persino superiore a 0,65. Ad esempio per
HD 222582 l’errore ammonta a circa il 20%.