È possibile enunciare e dimostrare il teorema fondamentale dell’aritmetica?

Teorema [Teorema Fondamentale dell’Aritmetica].
Ogni numero intero N 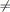0 può essere scritto come prodotto

N = c p₁ p₂ ^… p_k,

dove c = 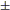1 e p_i > 0 sono numeri primi
(i = 1, …, k). Questa espressione è unica
a meno dell’ordine dei fattori.

Prima di procedere nella dimostrazione di questo
risultato, facciamo una serie di osservazioni, che ci permetteranno di
penetrarne meglio l’importanza ed eleganza, spesso offuscate dall’apparente
semplicità.

Che cosa si intende per numero
primo?
I numeri primi possono
essere considerati come i veri e propri “mattoni” su cui è costruita
l’intera aritmetica. La definizione è semplicissima: un numero intero
e positivo è primo se e solo se è divisibile soltanto per se
stesso e per 1 (ci limitiamo a considerare solo i divisori positivi).
Sottolineiamo che, per motivi che chiariremo in seguito, 0 e 1 non sono
considerati numeri primi.

È possibile dare una definizione alternativa di
numero primo:

Proprietà 1. Sia p un numero intero
positivo diverso da 0 e da 1; p è primo se e soltanto se,
ogni qualvolta p divide un prodotto ab, divide almeno uno dei due fattori
(cioè p divide a oppure p divide b).

Osserviamo immediatamente che questa condizione non è
più vera se p non è primo. Per esempio, 6 divide
4 ^. 3 = 12, ma non divide né 4 né
3.
Per la dimostrazione
dell’equivalenza di queste due definizioni (una delle due implicazioni viene
spesso citata in letteratura come Lemma di Euclide) rimandiamo alla
bibliografia consigliata. Osserviamo che questa definizione trova la sua
importanza nella possibilità di estendere il concetto di elemento primo
in ambienti più generali, di cui i numeri interi costituiscono un caso
particolare (domini d’integrità, domini euclidei, elementi primi ed
elementi irriducibili)

Quanti sono i numeri primi?

L’esistenza dei numeri primi è abbastanza ovvia, basta considerare 2
per esempio (è divisibile solo da 1 e 2!), oppure 3, 5, 7 etc… Un
fatto meno banale è che tali numeri sono infiniti. La
dimostrazione di questo fatto risale ad Euclide (300 a.C. circa) e si basa su
un procedimento ad absurdum (metodo indiretto). Supponiamo per assurdo
che i numeri primi siano finiti:
p₁, …, p_k e definiamo

M = p₁ p₂ ^… p_k + 1.

Questo numero è chiaramente diverso da tutti i
p_i e quindi — per ipotesi — deve essere divisibile da
almeno uno dei numeri primi precedenti (altrimenti sarebbe primo!). Ma questo
è impossibile in quanto il resto della divisione per uno qualsiasi dei
p_i è sempre 1. In altre parole, partendo
dall’ipotesi che i numeri primi sono in numero finito, si costruisce un nuovo
numero primo diverso dai precedenti. (Si veda anche una precedente risposta di Luca Fini)

Cerchiamo ora di comprendere meglio l’importanza del
teorema fondamentale dell’aritmetica.

      Consideriamo il seguente paragone.

      Possiamo pensare ai numeri interi
positivi come delle parole. Chi svolge il ruolo dell’alfabeto
in questo caso? Il teorema fondamentale dell’aritmetica ci dice che tale
ruolo è svolto dai numeri primi: ogni numero/parola può
essere scritto come prodotto/sequenza di numeri primi/lettere
(tralasciamo per un attimo la presenza della c dell’enunciato del
teorema: se il numero è positivo, c = +1). C’è
una differenza però. Mentre nel caso delle parole, ogni sequenza di
lettere determina unicamente la parola (un anagramma rappresenta una parola
diversa!), nel nostro caso cambiano l’ordine nel prodotto otteniamo lo stesso
numero (proprietà commutativa del prodotto). Per questo motivo si
parla di unicità a meno dell’ordine dei fattori, cioè
unicità dei “mattoni” che costituiscono il numero, ma non dell’ordine
con cui li disponiamo!
      Chiaramente lo
stesso ragionamento si applica ai numeri negativi, semplicemente scegliendo
c = -1.

Quanto detto sopra permette di dare una spiegazione (non
l’unica possibile!) al fatto che 1 non è considerato un numero primo.
Infatti, se lo considerassimo primo, perderemmo l’unicità anche a meno
dell’ordine. Più in dettaglio, se 1 fosse primo, potremmo includere
nella nostra rappresentazione un numero arbitrario di 1 (tanto moltiplicare
per 1 non altera il risultato finale) e quindi non avremmo più un unico
insieme di “mattoni” che definiscono il nostro numero. Per riprendere il
paragone di prima, è come se esistesse una lettera jolly * priva di
alcun suono e significato; in questo modo la parola NUMERO e la parola
**N*U****MER*O** sarebbero la stessa e non potremmo più parlare di
unicità di scrittura!

La scomposizione di un numero N nella forma
dell’enunciato del teorema prende il nome di scomposizione in fattori
primi (o irriducibili). Il teorema fondamentale dell’aritmetica ci
dice che tale fattorizzazione è unica (nel senso spiegato sopra).
L’insieme dei numeri interi rappresenta quindi un esempio di dominio a
fattorizzazione unica (UFD, dall’inglese Unique Factorization
Domain).
Questi domini sono stati
studiati in contesti più generali e astratti del caso numerico, quali
ad esempio anelli di polinomi, interi di Gauss etc. Per maggiori informazioni
su questi domini, rimandiamo alla bibliografia consigliata.

Veniamo ora alla dimostrazione del nostro Teorema.

Dimostrazione (teorema fondamentale dell’aritmetica).
Cominciamo dimostrando l’esistenza di una simile fattorizzazione.
Supponiamo che sia N > 0 (altrimenti basta prendere
c = -1 e considerare –N).

Escludiamo subito i casi banali:

N = 1. In tal caso abbiamo già
la scomposizione richiesta: basta prendere c = +1 e
k = 0.

N = p (p primo). In tal
caso la fattorizzazione è data da c = +1,
k = 1 e p₁ = p,
cioè:

N = (+1) ^. p.

Per dimostrare il risultato per ogni
N > 1, procederemo per induzione completa su N (per
maggiori informazioni su tale metodo, consultare qualsiasi testo tra quelli
citati in bibliografia).

Base induzione (N = 2). Questo caso
rientra tra i casi banali appena discussi (N è primo).

Passo induttivo. Assumiamo che il risultato sia vero
per tutti gli interi positivi minori di N. Dimostriamo che è
vero anche per N. Possiamo assumere che N non sia primo (in
questo caso sappiamo già che la fattorizzazione esiste, vedi i casi
banali sopra): allora esiste un divisore proprio di N, cioè
b < N tale che N = bq
(il resto della divisione è 0 in quanto stiamo assumendo che b
divida N). Entrambi b e q sono minori di N, e
quindi per l’ipotesi induttiva sappiamo che esiste una loro fattorizzazione.
La fattorizzazione di N sarà data mettendo insieme la
fattorizzazione di b e quella di q.

Questo completa la dimostrazione
dell’esistenza.

Mostriamo ora l’unicità (a meno dell’ordine) di
tale fattorizzazione.
Supponiamo che

p₁ p₂ ^… p_k =
N = q₁ q₂ ^… q_m.

Applichiamo la Proprietà 1 (vedi sopra) prendendo
p = p₁. Poiché p₁
è primo e divide il prodotto
(q₁ q₂ ^… q_m),
deve dividere uno dei fattori, per esempio q₁ (tanto non
siamo interessati all’ordine dei fattori, quindi possiamo cambiarlo in modo
che il fattore diviso da p sia proprio q₁). In
particolare q₁ è primo, quindi può essere
diviso solo da se stesso e dall’unità. Ne segue che
p₁ = q₁. Quindi possiamo
cancellare i due termini nel prodotto e otteniamo:

p₂ ^… p_k =
q₂ ^… q_m.

Possiamo iterare il procedimento prendendo
p₂ e cancellando un fattore che possiamo assumere essere
q₂, e così via fino a quando non “finiscono” i
fattori in uno dei lati dell’uguaglianza. Se
k < m, finiranno prima i fattori a sinistra e
otterremo quindi (a meno di riordinare i termini):

1 = q_k+1 ^… q_m,

che è impossibile in quanto i q_i
sono strettamente maggiori di 1 (e quindi il loro prodotto non può
essere uguale a 1).

Analogamente non si potrà
nemmeno avere k > m (in questo caso finirebbero
prima i fattori di destra e otterrei un’analoga contraddizione).

Quindi k = m,
cioè compare lo stesso numero di fattori (“mattoni”) in entrambe le
scomposizioni, ed in particolare (a meno di riordinarli) si ha

p₁ = q₁

^…

p_k = q_k

e questo conclude la dimostrazione dell’unicità.

Bibliografia suggerita:

M. Artin, Algebra, Prentice Hall (1991).

D. S. Dummit, R. M. Foote,
Abstract Algebra, Wiley (1999).

G. M. Piacentini Cattaneo, Algebra, un
approccio algoritmico, Decibel – Zanichelli (1996).