La domanda posta dal lettore si riferisce ad un famoso
studio pubblicato da Shannon nel 1949 riguardante la teoria dell’informazione
ed in particolare la teoria dei codici, scienza che si occupa del problema
riguardante la sicurezza della comunicazione tra due o più soggetti.
Questo problema può essere schematizzato come segue:
|
Alice e Bob (così sono chiamati in letteratura |
Questo problema è particolarmente importante per i
militari sui campi di battaglia in quanto i comandanti impartiscono gli
ordini ai subalterni mediante le radio ed è pertanto semplice per il
nemico intercettare le comunicazioni e venire a conoscenza delle tattiche
dell’avversario. Per ovviare a questo inconveniente, durante la seconda
guerra mondiale gli USA addestrarono molti pellerossa Navajo come soldati
addetti alle telecomunicazioni e li impiegarono nella guerra contro il
Giappone nel Pacifico. Ogni reparto aveva uno o due indiani navajo nel
proprio organico, e le truppe comunicavano tra loro parlando in questo
idioma, che era sconosciuto ai giapponesi. Per fare un esempio più
vicino al nostro mondo, anche le pay-tv trasmettono via “etere”, e tutti
quelli dotati dell’opportuna antenna possono ricevere il segnale trasmesso
dalle TV, ma solo chi ha il decoder può godersi lo spettacolo, proprio
perché le trasmissioni vengono criptate, ossia tradotte in un
opportuno codice che solo i decoder possono decifrare.
Lo studio pubblicato da
Shannon richiede conoscenze approfondite di matematica e soprattutto
dimestichezza con il calcolo delle probabilità, ed è quindi
opportuno trattare l’argomento suddividendolo in due parti: nella prima
l’argomento verrà discusso in modo discorsivo, mentre nella seconda la
trattazione sarà in po’ più tecnica e formale.
Parte I – Trattazione discorsiva
Già Giulio Cesare, quando scriveva ordini importanti
ai suoi alti ufficiali, non li scriveva in chiaro ma li codificava con il
cosiddetto cifrario di Cesare, che consiste nel sostituire ogni
lettera del messaggio con quella dell’alfabeto che la succede di tre posti.
Così facendo alla lettera A si sostituisce la D, alla B la E, alla C
la F e cosi via. Considerando l’alfabeto a 26 lettere (che qui riporto per
comodità del lettore: ABCDEFGHIJKLMNOPQRSTUVWXYZ), alla lettera W
corrisponde la Z, alla X la A, alla Y la B e alla Z la C, quindi ad esempio,
la parola “IMPERATORE” si trasforma in “LPSHUDWRUH“. Invece di considerare spostamenti in
avanti di 3 posti, si possono anche considerare spostamenti di 4, 5, 6 ecc.
posti, anche se comunque, è facile intuire che per qualsiasi spione
è un gioco da ragazzi riuscire a decifrare un messaggio codificato in
questo modo molto semplice.
Il numero di posizioni
in avanti cui si devono spostare le lettere per cifrare il messaggio è
detto chiave di cifratura, ed essendo palese che è inutile
considerare spostamenti superiori a 26 posti, le chiavi possibili sono 26.
Uno stratagemma che è possibile adottare per rendere la vita
più difficile a chi cerca di decifrare il messaggio è quello di
spostare le lettere in posizione dispari di un certo numero di posizioni (ad
esempio 2) e quelli in posizioni pari di un altro numero di posti (ad esempio
4): così facendo, con le scelte operate, la parola “IMPERATORE” diviene “KQRITEVSTI“. La coppia di numeri
(2, 4) forma la chiave del codice, ed è quindi chiaro che con
questo accorgimento le possibili chiavi di cifratura sono
262 = 676.
Per rendere ancora
più difficile l’opera di decifrazione, invece di usare una chiave
formata da una coppia di numeri è possibile usare una chiave formata
da una terna di numeri, in modo che le lettere nella 1o,
4o, 7o, 10o… posizione si spostano di un
certo numero n di passi (ad esempio 3), le lettere nella
2o, 5o, 8o, 11o… posizione
avanzano di un altro numero m di passi (ad esempio 5) e quelle nella
posizione 3o, 6o, 9o, 12o… di
p passi (ad esempio 2). Con la chiave (3, 5, 2) la parola
“IMPERATORE” diviene LRRHWCWTTH. Naturalmente i numeri
n, m, p devono essere minori di 26, e quindi in questo
caso il numero delle chiavi possibili è
263 = 17576.
Con lo stesso principio
si possono considerare chiavi più lunghe, ed è abbastanza
evidente che più lunga è la chiave maggiore è la
difficoltà di decifrare il testo di chi non conosce né la
parola chiave, né tanto meno la sua lunghezza. Naturalmente, la chiave
con cui il mittente Bob cifra il messaggio deve essere nota anche alla
ricevente Alice e soprattutto non deve essere nota a nessun altro.
Questo modo di cifrare i
messaggi è stato ideato da Vignere e viene detto appunto cifratura
di Vignere. Benché sia stata considerata inviolabile per molti
anni, nel 1863 essa è stata violata, ossia è stato trovato un
procedimento per decifrare i messaggi criptati, senza avere informazioni a
priori circa la chiave, da Kasiski, sfruttando il punto debole di questa
cifratura, ossia la lunghezza della chiave. Senza scendere in dettagli
tecnici, diciamo soltanto che se la chiave è corta rispetto alla
lunghezza del messaggio, nel testo cifrato compaiono degli indizi che
permettono agli esperti di crittoanalisi di poter, sia pur con
difficoltà, decifrare il messaggio. Maggiore è la lunghezza
della chiave, maggiore sono le difficoltà in cui s’imbattono i
crittoanalisi per decifrare il testo. Se la lunghezza della chiave è
pari a quella del testo, allora i crittoanalisti non hanno “appigli” per
tentare di decifrare il messaggio. Un cifrario di Vignere in cui la lunghezza
della chiave è uguale alla lunghezza del messaggio è detto
cifrario di Verman.
I sistemi di cifratura
descritti fino a questo punto sono detti a chiave simmetrica
giacché si usa la stessa chiave sia per cifrare sia per decifrare il
messaggio, mentre esistono altri metodi di cifratura che utilizzano due
chiavi diverse, una per cifrare e l’altra per decodificare. Tali tipi di
sistemi sono detti a chiave asimmetrica e il più famoso di essi
si chiama RSA. Al
momento, non è stato trovato ancora alcun metodo per decodificare un
messaggio cifrato con il sistema RSA, però nell’arco dei secoli sono
stati ideati molteplici tipi di cifrature, le quali sono state quasi tutte
violate dagli esperti della crittoanalisi i quali, partendo dal testo
cifrato, con abilità, pazienza e perizia, hanno individuato i punti
deboli delle varie tecniche crittografiche e hanno permesso la decifrazione
dei messaggi codificati con tali tecniche.
Definizione. Un sistema crittografico si dice
perfetto se, partendo da un qualsiasi testo cifrato con il metodo in
questione, è impossibile risalire al testo originario (testo in
chiaro) senza conoscere la chiave di decifrazione, indipendentemente dalla
quantità del testo cifrato e delle risorse computazionali a
disposizione dei crittoanalisi, mentre è molto agevole decifrarlo
conoscendo quest’ultima.
Il cifrario di Verman
è un cifrario perfetto, e tale risultato discende proprio dal teorema
di Shannon il quale afferma che:
|
in un cifrario perfetto la lunghezza della chiave deve |
Adesso cercheremo di formalizzare quanto fino a questo
momento affermato fornendo una trattazione teorica dell’argomento, enunciando
il teorema di Shannon e fornendo una sua dimostrazione.
Parte Seconda – Trattazione formale
Definizione. Un crittosistema è una
quintupla
(M, C, K, Ek, Dk),
dove
-
M è l’insieme dei testi in chiaro, detti
anche plaintext; -
C è l’insieme dei testi cifrati, detti anche
chiptext; -
K è l’insieme delle possibili chiavi;
-
Ek è la funzione di cifratura
(funzione della chiave k e di m, dove
k K e
K e
m M);
M);
-
Dk è la funzione di decifratura
(funzione della chiave k e di c, dove
k K e
K e
c C).
C).
Notiamo che, secondo la definizione e come precedentemente
annunciato, si può cifrare un messaggio con una chiave k e
decifrarlo con una chiave k’ diversa. La funzione
Ek : M –> C deve
essere necessariamente iniettiva, ossia invertibile a sinistra, e deve
esistere una chiave k’ tale che
Dk’(Ek(m)) = m
per ogni m  M. Se
M. Se
k = k’ il crittosistema è detto
simmetrico, mentre nell’altro caso è detto asimmetrico
con k chiave pubblica e k’ chiave privata.
Nella teoria introdotta
da Shannon si assume che i processi di generazione del plaintext m,
della chiave k e del chiptext c, siano descritti da tre
variabili casuali discrete XM, XK e
XC con distribuzione di probabilità nota. Si assume
che XM e XK siano indipendenti e che ogni
elemento m  M e ogni elemento
M e ogni elemento
k  K abbiano probabilità
K abbiano probabilità
non nulla di essere generati, ossia deve essere
P(XM = m) > 0 per ogni
m  M e
M e
P(XK = k) > 0 per ogni
k  K. Da notare invece che, al
K. Da notare invece che, al
contrario, XM e XC, così come
XK e XC, non sono necessariamente
indipendenti.
Definizione. Un cifrario è detto
perfetto se e accade che
P(XM = m | XC = c) = P(XM = m)
per ogni m  M,
M,
c  C.
C.
Il significato di questa definizione è praticamente
identico a quanto scritto in modo alquanto informale nella precedente
definizione, ossia: la probabilità che il plaintext sia un certo
m è uguale alla probabilità che il messaggio sia
m data la conoscenza del chiptext c, ossia la conoscenza del
chiptext non dà all’analista alcuna informazione in più per
individuare il messaggio rispetto a quello a quello che avrebbe tirando a
indovinare.
Teorema (Shannon). In ogni cifrario perfetto,
|K| > |M|.
Nel caso in cui, per la costruzione delle chiavi k e
dei messaggi m, si usa lo stesso alfabeto, ossia lo stesso insieme di
simboli, la condizione implica che la lunghezza della chiave k deve essere
maggiore o uguale alla lunghezza del testo m che intendiamo inviare.
Dimostrazione. Essendo Ek
iniettiva, allora deve essere |C| 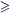 |M|. Se per assurdo fosse
|M|. Se per assurdo fosse
|K| < |M| 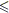 |C|, allora per ogni m
|C|, allora per ogni m  M esisterebbe un cm
M esisterebbe un cm  C che non può essere generato da
C che non può essere generato da
m per nessuna chiave k  K, ossia cm
K, ossia cm 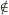 {Ek(m) | k
{Ek(m) | k  K} (infatti,
K} (infatti,
|{Ek(m) | k  K}|
K}| 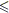 |K|). Per definizione di cifrario perfetto
|K|). Per definizione di cifrario perfetto
avremmo allora che
P(XM = m) = P(XM = m | XC = cm) = 0,
contro il fatto che deve essere
P(XM = m) > 0 per ogni
m  M. La dimostrazione segue
M. La dimostrazione segue
allora per assurdo.
Esempio di cifrario perfetto. Il codice One time
Pad (letteralmente, “blocchetto monouso”) è stato introdotto, come
già detto in precedenza, da Vernam nel 1917 e ottenuto estremizzando
il discorso sulla chiave del cifrario di Vignere, scegliendo appunto una
chiave lunga quanto il testo. Sembra che questo codice sia stato usato per
criptare le comunicazioni che avvenivano tra la Casa Bianca ed il Cremlino
negli anni della guerra fredda. Nella pratica, il plaintext m viene
preventivamente trasformato in formato digitale (ad esempio usando il codice
ASCII) ossia come sequenza di bit (0, 1), e sommato poi bit a bit alla
chiave k, preventivamente generata in maniera casuale (anch’essa in
formato digitale). L’operazione di somma bit a bit è definita come
segue: 0 + 0 = 0, 0 + 1 = 1,
1 + 0 = 1, 1 + 1 = 0. Ad esempio, se
m = (1, 0, 0, 1, 0, 1, 0, 1)
e
k = (1, 1, 0, 0, 1, 0, 1, 1)
allora
c = (0, 1, 0, 1, 1, 1, 1, 0).
Il ricevente ottiene il plaintext m eseguendo l’operazione di somma
bit a bit sopra definita tra c e k. Ai lettori più
attenti non sarà sfuggito che questo è un cifrario (simmetrico)
di Verman con un alfabeto composto di due soli caratteri.
Impaginato da Gino Favero