Come si puo’ dimostrare in modo rigoroso la correttezza dell’algoritmo “classico” di divisione tra numeri naturali che si impara nelle scuole elementari (detto talvolta “metodo della caravella”)?

Ricordiamo che l’insieme dei numeri naturali è un
dominio euclideo, cioè, dati due qualsiasi numeri naturali
a e b con b 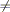 0
(detti rispettivamente dividendo e divisore) esiste un’unica
coppia di numeri naturali (q, r) (detti rispettivamente
quoziente e resto) tali che
a = bq + r e 0 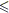 r < b. Si dice
allora (con una locuzione leggermente scorretta dal punto di vista matematico
ma molto affermata e sufficientemente chiara da non generare troppa
confusione) che a diviso b è uguale a q con il
resto di r. Così, per esempio,
21357 : 18 = 1186 con il resto di 9, perché
21357 = 18 ^. 1186 + 9.

      Il “metodo della
caravella” è un algoritmo per ottenere il quoziente e il resto di una
divisione euclidea. Ne do qui di seguito una descrizione leggermente
differente da quella data abitualmente nelle scuole elementari ma più
“formale” e efficace dal punto di vista schematico (la descrizione potrebbe
sembrare un po’ nebulosa in un primo momento, ma dovrebbe diventare chiara
dopo l’esempio che la segue successivamente).

1. disegniamo una tabella come nella figura qui sotto, dove
   si collocano il dividendo in alto a sinistra, il divisore in alto a destra e
   si creano sotto il divisore tante caselle quante sono le cifre del dividendo;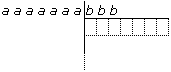

   
   

2. definiamo n = 1;

3. consideriamo il numero a_n formato
   dalle prime n cifre del numero che si trova nella riga più in
   basso della colonna di sinistra;

4. scriviamo nell’n-esima casella sotto il divisore
   il quoziente della divisione euclidea tra a_n e il divisore;
   aggiungiamo inoltre una riga alla prima colonna, scrivendo il numero che si
   ottiene sostituendo il resto della divisione euclidea tra
   a_n e il divisore alle prime n cifre del numero che
   si trova nella riga precedente (aggiungendo eventualmente degli zeri
   all’inizio del numero, in modo da avere nella colonna di sinistra numeri che
   hanno tutti lo stesso numero di cifre);

5. se n è pari al numero delle cifre del
   dividendo, passiamo al punto 6.; altrimenti, aumentiamo n di
   un’unità e torniamo al punto 3;

6. il numero scritto sotto il divisore è il
   quoziente e l’ultima riga della colonna di sinistra è il resto.

Prima di illustrare l’esempio promesso, vale subito la pena
di fare un commento. Nel punto 4. si chiede di effettuare una divisione
euclidea tra il numero a_n e il divisore dell’operazione
originaria. Questo potrebbe sembrare disonesto, perché dà un
metodo per risolvere una divisione euclidea che usa la soluzione di
una divisione euclidea. In realtà il “trucco” sta nel fatto che le
divisioni euclidee che si effettuano al punto 4. sono particolarmente
“semplici” — in un senso che preciseremo meglio più avanti — e
quindi (a differenza di una divisione come la già citata
21357 : 18) si possono risolvere con metodi particolarmente
diretti.

      Proviamo a applicare
l’algoritmo appena descritto proprio alla divisione 21357 : 18:

• iniziamo a disegnare lo schema descritto nel punto 1.
  dell’algoritmo. Sotto il divisore dobbiamo lasciare cinque caselle libere,
  perché il dividendo ha cinque cifre;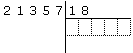

  
  

• passiamo al punto 2. e definiamo n = 1;

• passiamo al punto 3. e consideriamo il numero formato
  dalla prima cifra del numero che si trova nell’ultima riga (che è
  anche la prima!) della colonna di sinistra, cioè
  a₁ = 2. La divisione euclidea tra 2 e 18
  dà quoziente 0 e resto 2;

• come richiesto dalla prima parte del punto 4., scriviamo
  0 nella prima casella sotto il divisore;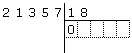

  
  

• ligi al dovere e obbedienti alla seconda parte del punto
  4., scriviamo quindi un nuovo numero nella colonna di sinistra sostituendo la
  prima cifra di 21357 (che è 2) con il resto della divisione di cui
  sopra (che è ancora 2, quindi per il momento non è cambiato
  nulla…);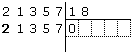

  
  

• dal momento che n è ancora minore di
  cinque, aumentiamolo di 1 (ottenendo quindi n = 2) e
  torniamo al punto 3.;

• il numero formato dalle prime due cifre del numero
  nell’ultima riga (che ora è la seconda) è
  a₂ = 21. La divisione euclidea tra 21 e 18
  dà quoziente 1 e resto 3: dobbiamo allora scrivere 1 nella seconda
  casella sotto il divisore e scrivere una nuova riga nella prima colonna
  sostituendo le prime due cifre di 21357 (cioè 21) con il resto della
  divisione, cioè 03;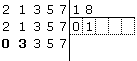

  
  

• n è ancora minore di cinque, quindi
  poniamo n = 3 e torniamo al punto 3;

• abbiamo ora
  a₃ = (0)33 = 1 ^. 18 + 15;
  scriviamo allora 1 nella terza casella sotto il divisore e un nuovo numero
  nella prima colonna sostituendo le prime tre cifre di 03357 (cioè 033)
  con 015;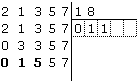

  
  

• torniamo al punto 3. dopo avere posto
  n = 4;

• otteniamo
  a₄ = (0)155 = 8 ^. 18 + 11;
  scriviamo allora 8 nella quarta casella sotto il divisore e il numero 00117
  nella prima;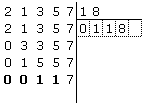

  
  

• poniamo n = 5 e torniamo al punto 3.;

• abbiamo otteniamo
  a₅ = (00)117 = 6 ^. 18 + 9,
  quindi scriviamo 6 nella quinta casella sotto il divisore e 00009 nella
  prima;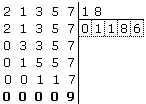

  
  

• n è pari al numero delle cifre del
  dividendo, quindi passiamo al punto 6.;

• il quoziente è (0)1186 e il resto è
  (0000)9.

Ora che (auspicabilmente) è più chiaro il
significato dell’algoritmo così come l’ho descritto sopra, occupiamoci
di dimostrarne la correttezza. In particolare, dobbiamo dimostrare che
l’algoritmo termina in un numero finito di passi e che il risultato che si
ottiene è sempre corretto (cioè che i numeri ottenuti alla fine
sono proprio il quoziente e il resto della divisione euclidea tra il
dividendo e il divisore); già che ci siamo, inoltre, è il caso
di spiegare che cosa intendevo quando dicevo che le divisioni da effettuare
nel punto 4. sono “semplici”.

     Il fatto che l’algoritmo
termini in un numero finito di passi è il più semplice da
dimostrare. Indichiamo con c il numero di cifre del dividendo: si
noti che la fase iterativa (quella, cioè, in cui si stanno ripetendo
le stesse istruzioni già eseguite in precedenza, seppure applicandole
a dati ogni volta diversi, e che è formata dai tre passi 3., 4. e 5.)
viene ripetuta soltanto finché n è minore di c.
Allora, dal momento che all’inizio dell’algoritmo si pone
n = 1 (passo 2.) e che a ogni iterazione n viene
incrementato di un’unità (passo 5.), tale fase viene ripetuta
esattamente c volte, quindi vengono eseguite esattamente
2 + 3c + 1 = 3(c + 1)
istruzioni, un numero finito.

      Dimostriamo ora due
proprietà importanti di questo algoritmo:

1. in ogni momento dell’esecuzione, moltiplicando il
   divisore per il numero che si trova sotto il divisore (considerando le
   caselle vuote come zeri) e aggiungendo al prodotto il numero che si trova in
   fondo alla prima colonna, si ottiene il dividendo;

2. all’n-esimo passaggio per il punto 5., il numero che
   si trova in fondo alla prima colonna è minore del divisore
   moltiplicato per 10^c–n, dove c (come
   sopra) è il numero di cifre del dividendo.

Si noti che in effetti queste proprietà sono
soddisfatte nell’esempio visto sopra: iterazione per iterazione, si ha
infatti:

1.   21357 = 18 ^. 00000 + 21357,      21357 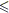 180000,
2.   21357 = 18 ^. 01000 + 03357,      03357 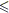 18000,
3.   21357 = 18 ^. 01100 + 01557,      01557 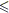 1800,
4.   21357 = 18 ^. 01180 + 00117,      00117 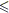 180,
5.   21357 = 18 ^. 01186 + 00009,      00009 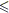 18.

Per dimostrarle in generale usiamo il metodo per induzione,
secondo il quale se una famiglia di proposizioni P₀,
P₁, …, P_c è tale che
P₀ è vera e che P_n segue da
P_n-1 per ogni n = 1, …,
c, allora tutte le P_n sono vere. Come indice
n della famiglia di proposizioni, usiamo proprio il numero n
definito nell’algoritmo, con la convenzione ausiliaria che n sia
uguale a zero nel momento in cui si esegue l’istruzione 1. (e quindi n
non è ancora stato inizializzato) e che l’istruzione 1. costituisca
quindi la “0-esima iterazione” dell’algoritmo. Le proposizioni che vogliamo
dimostrare sono allora:

• P_n: alla fine dell’n-esima
  iterazione, moltiplicando il divisore per il numero che si trova sotto il
  divisore (considerando le caselle vuote come zeri) e aggiungendo al prodotto
  l’(n + 1)-esima riga della prima colonna, si ottiene
  il dividendo;

• Q_n: alla fine dell’n-esima
  iterazione, l’(n + 1)-esima riga della prima colonna
  è minore del divisore moltiplicato per
  10^c–n,

con n che varia da 0 a c. Procediamo in
questo modo:

• Quando l’algoritmo inizia, il numero sotto il divisore
  è 0 e la prima riga della tabella è il dividendo a.
  Qualsiasi sia il divisore b, di certo
  a = b ^. 0 + a,
  quindi P₀ è vera. Inoltre, è sempre vero che
  un numero di c cifre è minore di 10^c (che ha
  c + 1 cifre!), quindi, dato che b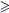  1,
  a < 10^c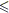  b ^. 10^c,
  cioè anche Q₀ è vera.

• Supponiamo ora per ipotesi induttiva che
  P_n-1 e Q_n-1 siano vere (con
  n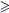  1). Chiamando
  x_n-1 la n-esima riga della tabella e
  y_n-1 il numero formato dalle cifre scritte nelle
  prime n – 1 caselle sotto il divisore (cioè, i numeri
  determinati alla fine dell'(n – 1)-esima iterazione), ci si
  convince che l’ipotesi si traduce nelle due relazioni

  a = b ^. y_n-1 ^. 10^c–n+1 + x_n-1,
        
  x_n-1 < b ^. 10^c–n+1.

  Vediamo ora che cosa succede alla n-esima iterazione.
  Chiamare a_n il numero formato dalle prime n cifre di
  x_n-1 (passo 3.) permette di scrivere

  x_n-1 = a_n ^. 10^c–n + a’_n,

  dove a’_n è il numero formato dalle
  ultime c – n cifre di x_n-1 e
  soddisfa le relazioni 0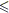  a’_n < 10^c–n.

  La divisione euclidea tra a_n e b (passo 4.)
  dà due numeri q_n e r_n tali che
  a_n = bq_n + r_n
  e 0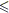  r_n < b. Si noti che
  deve essere per forza q_n < 10: se così
  non fosse (cioè se fosse q_n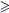  10), combinando tutte le relazioni note si avrebbe infatti

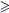
  xn-1 = an . 10c–n + a’n = (bqn + rn) . 10c–n + a’n xn-1  (b .10 + 0) . 10c–n + 0 = b . 10c–n+1,

  contro l’ipotesi induttiva che
  x_n-1 < b ^. 10^c–n+1.
  Allora q_n è un numero formato da una sola cifra.

        Alla fine del passo 4.,
  si hanno i nuovi numeri x_n (in fondo alla prima colonna) e
  y_n (formato dalle cifre scritte nelle prime n
  caselle sotto il divisore) costruiti in questo modo:

  x_n := r_n ^. 10^c–n + a’_n,
        
  y_n := y_n-1 ^. 10 + q_n.

  Tenendo presente queste relazioni e l’ipotesi induttiva si
  ha allora

  b . yn . 10c–n + xn = b . (yn-1 . 10 + qn) . 10c–n + rn . 10c–n + a’n b . yn . 10c–n + xn = b . yn-1 . 10c–n+1 + (bqn + rn) . 10c–n + a’n b . yn . 10c–n + xn = b . yn-1 . 10c–n+1 + (an . 10c–n + a’n) b . yn . 10c–n + xn = b . yn-1 . 10c–n+1 + xn-1 = a,

  quindi P_n è vera. In modo analogo,

  x_n = r_n ^. 10^c–n + a’_n
  <
  r_n ^. 10^c–n + 10^c–n
  =
  (r_n + 1)^. 10^c–n
  
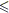
  b ^. 10^c–n,

  quindi anche Q_n è vera.

Queste proposizioni permettono allora di concludere che
l’algoritmo è corretto, perchè all’ultima iterazione
restituisce due numeri x_c e y_c tali che
a = by_c+ x_c (per la
proposizione P_c, ricordando che
10^c–c = 10⁰ = 1) e
x_c < b (per la proposizione
Q_c allo stesso modo). In altre parole,
x_c e y_c soddisfano le proprietà
del resto e del quoziente di a : b e quindi, per
l’unicità del risultato della divisione euclidea, sono il
quoziente e il resto di a : b.

      Nel corso della
dimostrazione del passo induttivo, inoltre, siamo anche riusciti a vedere che
cosa rende particolarmente “semplici” le divisioni che si effettuano al passo
4. dell’algoritmo: il loro quoziente è sempre minore di 10. È
allora possibile risolvere quelle divisioni, per esempio, con un metodo di
“ricerca del multiplo”, cioè confrontando con il divisore i primi 10
multipli di b (da b ^. 0 a
b ^. 9) e prendendo come quoziente il fattore
q corrispondente al più grande multiplo minore del dividendo
(al lettore volenteroso il compito di tradurre questo metodo in un algoritmo
e verificarne la correttezza!). In altre parole, il “metodo della caravella”
serve a ridurre una divisione euclidea di due qualsiasi numeri naturali a
più divisioni euclidee tra due numeri naturali tali che il dividendo
non sia mai superiore al decuplo del divisore.