Nelle scienze naturali e tecniche si ha spesso a che fare
con processi periodici quali, per esempio, il moto periodico dei corpi
celesti e delle particelle elementari, le vibrazioni acustiche ed
elettromagnetiche, il moto oscillatorio e rotatorio di varie parti delle
macchine e dei congegni etc… Tali processi hanno sempre attirato e
incuriosito l’attenzione dei fisici e dei matematici, proprio per questo loro
“eterno ripetersi”, che permette di conoscere (in ogni istante) quella che
è stata la loro evoluzione passata e quella che sarà la loro
evoluzione futura.
Dal punto di vista
matematico, tutti i processi del genere sono descritti da funzioni
periodiche, funzioni che possono essere intuitivamente definite nel seguente
modo:
Definizione 1. Una funzione f(t)
(definita su tutto 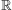 ) si dice
) si dice
periodica se esiste un numero T 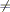 0
0
(detto periodo della funzione) tale che
f(t + T) = f(t) per
ogni t 
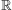 .
.
Osservazione 1. In realtà la definizione
così data di periodo è un po’ sbrigativa e non univoca.
Infatti, in questo modo, anche 2T, 3T, … sarebbero periodi
della nostra funzione e non si esclude la possibile esistenza di un altro
periodo S tale che 0 < S < T
che soddisfi la stessa proprietà. Per risolvere questo problema (e
quindi dare una definizione di periodo che non lasci spazio ad
ambiguità di alcun genere), definiremo il periodo della funzione come
il minimo T > 0 che soddisfi la proprietà
sopra menzionata, cioè:
min {T > 0 | f(t + T) = f(t)
per ogni t 
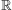 }.
}.
Il problema relativo all’esistenza di questo minimo è
tutt’altro che banale: se f è periodica, che esista l’estremo
inferiore è sempre vero e questo sarà sempre non negativo; il
problema è se questo è anche un minimo per l’insieme e se
è strettamente positivo. Osserviamo che nel caso della funzione di
Dirichlet
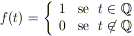
si ha che l’insieme
{T > 0 | f(t + T) = f(t)
per ogni t 
 } è
} è
l’insieme di tutti i numeri razionali positivi, quindi l’estremo inferiore
è 0.
Nel nostro caso
supporremo di lavorare con funzioni per cui tale minimo esiste ed è
positivo, anche se ci si rende facilmente conto che le dimostrazioni che
seguiranno, non dipendono in alcun modo dalla scelta del “periodo minimale”,
cioè continuano ad essere valide se applicate con un qualsiasi
T > 0 che soddisfa la proprietà di cui sopra.
Le funzioni periodiche più semplici e note sono
le funzioni trigonometriche sin(t) e cos(t), con periodo
T = 2 . Osserviamo che da un punto di vista
. Osserviamo che da un punto di vista
fisico, tali funzioni sono legate alle cosiddette “armoniche” (o
vibrazioni armoniche) che rappresentano i più semplici e
interessanti moti periodici studiabili:
x(t) = A sin(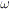 t + p);
t + p);
queste sono chiaramente funzioni periodiche di periodo
T = 2 /
/ 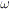
(detto periodo dell’armonica) e le costanti A, 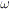 e p si dicono rispettivamente ampiezza,
e p si dicono rispettivamente ampiezza,
frequenza e fase iniziale dell’armonica.
Osserviamo che se una
funzione f(x) è periodica di periodo T, allora le
possiamo associare una nuova funzione
g(x) := f(Tx / 2 ), periodica di periodo 2
), periodica di periodo 2 . Questa osservazione
. Questa osservazione
ci permette di considerare (in seguito) solamente le funzioni periodiche con
periodo 2 e di dimostrare per queste i risultati di
e di dimostrare per queste i risultati di
convergenza per le serie di Fourier associate. La generalizzazione ad una
qualsiasi funzione periodica di periodo generico T è immediata,
considerando il cambio di variabile sopra introdotto.
Il problema principale che vogliamo ora trattare
è il problema della rappresentazione di una funzione periodica
arbitraria sotto forma di somme di armoniche, limitandoci ad
analizzare alcuni semplici risultati e ad accennare alcune interessanti
problematiche connesse. Tale limitazione è dettata dalla
vastità e complessità dell’argomento, che richiede la
conoscenza di nozioni e tecniche dell’analisi funzionale, che possono mancare
ad un lettore (per quanto acuto e interessato) di tale rubrica.
Questo affascinante
problema deve il suo principale contributo al lavoro di Joseph Fourier
(1768-1830), il quale nel suo “Théorie analytique de la
chaleur” (1822) sviluppa sistematicamente le sue idee e intuizioni. Il
contributo principale di Fourier consistette nell’idea (già adombrata
da Daniel Bernoulli) che una funzione periodica f(x) potesse
venir rappresentata mediante una serie della forma:
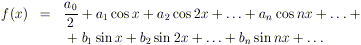
con opportuni coefficienti a0,
a1, …, b1, … (il ruolo, del tutto
formale, del fattore 1 / 2 davanti alla costante
a0 apparirà chiaro in seguito).
Questa espressione
è oggi nota col nome di serie di Fourier. Vedremo che una
siffatta rappresentazione di una funzione mediante una serie trigonometrica,
offre la possibilità di studiare tipi di funzioni considerevolmente
più generali di quanto consentito dalla serie di Taylor: anche se in
molti punti non esiste la derivata o la funzione non è continua, la
funzione (sotto opportune ipotesi) potrà lo stesso essere sviluppabile
attraverso una simile serie trigonometrica. Osserviamo che per sviluppare
una funzione attraverso la sua serie di Taylor, era necessario (ma non
certamente sufficiente) che la funzione fosse 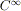
(cioè derivabile infinite volte, con derivate di ogni ordine
continue); le funzioni che ammettono tale rappresentazioni sono dette
analitiche (sono chiaramente un sottoinsieme proprio delle funzioni
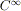 ). Nel caso delle serie di Fourier, vedremo come le
). Nel caso delle serie di Fourier, vedremo come le
condizioni di regolarità da richiedere siano in realtà molto
più deboli.
Vediamo ora di entrare
nei dettagli. Vogliamo studiare la possibilità di “sviluppare” una
funzione periodica f(x) (che per semplicità supporremo
di periodo 2 ) attraverso una serie trigonometrica della
) attraverso una serie trigonometrica della
forma
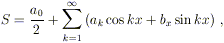
cioè cercare di approssimare tale funzione con dei
polinomi trigonometrici
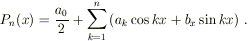
I problemi che vogliamo discutere possono così essere
riassunti:
-
determinare chi sono i valori candidati per
ak e bk (tali valori dovranno
evidentemente dipendere dalla funzione f); -
determinare le condizioni affinché la serie
così definita converga puntualmente alla funzione f,
cioè tali che: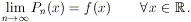
Cominciamo discutendo il primo punto. A tal fine ricordiamo
il seguente risultato (che si mostra semplicemente per induzione, integrando
più volte per parti):
Lemma 1. Valgono le seguenti relazioni:
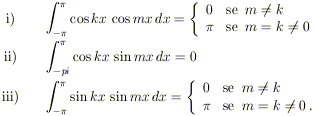
Al fine di determinare i “candidati” ad essere i
coefficienti della serie di Fourier S associata ad f,
supponiamo di conoscere tale serie e di sapere che tale serie converge
uniformemente alla funzione f:
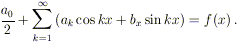
Moltiplichiamo ora entrambi i membri dell’equazione sopra
per cos(mx) (con m numero naturale) ed integriamo fra – e
e  , cioè su un periodo della funzione
, cioè su un periodo della funzione
(sarebbe stato equivalente integrare su un generico intervallo
[a, a + 2 )). Portando
)). Portando
l’integrale all’interno della sommatoria (cosa resa “lecita” dal fatto che
per ipotesi la serie S converge uniformemente), otteniamo:
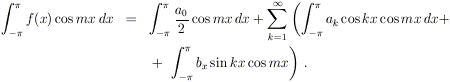
Usando ora il lemma enunciato in precedenza, possiamo
concludere che:
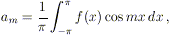
che vale anche per m = 0 in virtù
del fattore 1 / 2, inserito ad hoc nell’espressione della
serie. Analogamente, ripetendo lo stesso procedimento di prima,
moltiplicando questa volta per sin(mx), si ottiene:
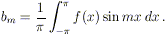
I coefficienti ak e bk
si chiamano coefficienti di Fourier relativi alla funzione
f(x). Osserviamo che per come sono stati definiti tali
coefficienti, questi sono apparentemente indipendenti (in
realtà dei legami esistono) dalla regolarità della f:
dipendono solo dalla sua integrabilità, cioè è
sufficiente che la funzione sia integrabile nell’intervallo [- ,
,  ). Questo permette di definire la
). Questo permette di definire la
serie di Fourier (almeno come serie formale) per una vasta gamma di funzioni
(non necessariamente continue); altro è il problema della convergenza
delle serie così definite.
Mostreremo ora un
teorema di convergenza sotto ipotesi (abbastanza deboli) di
regolarità, cioè nel caso di funzioni regolari a tratti.
Definizione 2. Sia f una funzione
periodica di periodo 2 . Diremo che f è
. Diremo che f è
regolare a tratti se:
-
è continua in [-
 ,
,  ) tranne al più in un numero finito di punti
) tranne al più in un numero finito di punti 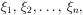 nei quali esistono finiti i limiti destro e sinistro;
nei quali esistono finiti i limiti destro e sinistro;
cioè per ogni i = 1, …, N: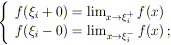
-
ha derivata continua eccetto nei punti
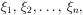 ed eventualmente in altri punti
ed eventualmente in altri punti 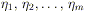
(sempre in numero finito); - è limitata.
Prima di arrivare a dimostrare il risultato principale,
enunceremo alcuni risultati preliminari e cercheremo di fornire un accenno
della loro dimostrazione.
Lemma 2. Vale la seguente relazione:
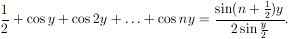
Dimostrazione. Procediamo per induzione.
-
BASE INDUZIONE: per n = 0
l’identità sopra diventa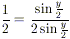
che è chiaramente vera.
-
PASSO INDUTTIVO: supponiamo che l’uguaglianza sia vera
per n – 1 e dimostriamola per n. Si ha: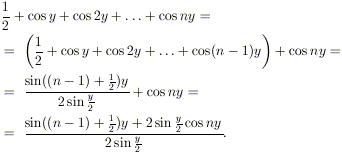
Ricordando che (stiamo
usando le formule di addizione per il seno)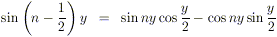
e sostituendo nell’espressione ottenuta
sopra, possiamo ottenere la tesi per n.
Osservazione 2. Questa uguaglianza ci permette anche
di concludere un altro fatto:
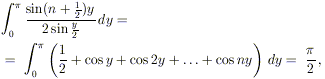
dove nell’ultimo passaggio abbiamo usato che (per
k 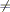 0):
0):
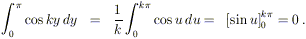
Analogamente si fa vedere che
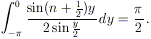
Dimostriamo ora un secondo lemma che riveste una grande
importanza, soprattutto nella teoria avanzata delle serie di Fourier.
Lemma 3 (Disuguaglianza di Bessel). Sia
F(t) una funzione integrabile e periodica di periodo
2 e siano ak, bk i suoi
e siano ak, bk i suoi
coefficienti di Fourier. Si ha:
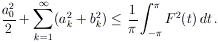
Dimostrazione. Si consideri la somma
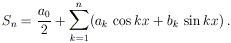
Si ha evidentemente (in quanto l’integrando è una
funzione non negativa)
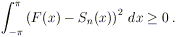
Ricordando le espressioni dei coefficienti di Fourier, si
ottiene:
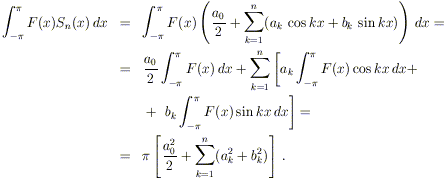
Analogamente, tenendo conto del lemma ![]() :
:
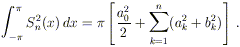
Quindi, mettendo assieme tutti i risultati ottenuti:
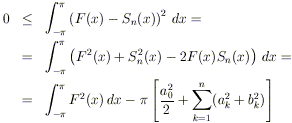
e di conseguenza:
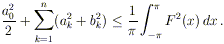
Passando al limite per n che tende all’infinito si
ottiene la tesi.
Osservazione 3. Il risultato precedente ci
permette di concludere un’interessante proprietà dei coefficienti di
Fourier (che è quella che useremo effettivamente per dimostrare il
nostro risultato di convergenza). Supponiamo che F sia una funzione
di quadrato integrabile (cioè 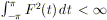 ); allora segue dalla disuguaglianza del lemma precedente che
); allora segue dalla disuguaglianza del lemma precedente che
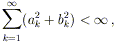
e quindi (per la condizione necessaria di Cauchy per la
convergenza di una serie) possiamo concludere
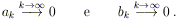
Di conseguenza:
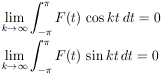
per ogni funzione di quadrato integrabile in [- ,
,  ). È importante notare che tale
). È importante notare che tale
risultato continua ad essere valido (ma con dimostrazione meno immediata)
anche nel caso in cui la F sia soltanto integrabile (si veda il
lemma di Riemann-Lebesgue, per la cui dimostrazione rimandiamo ai testi
consigliati in bibliografia).
Concludiamo questa (breve) rassegna di risultati
tecnici, enunciando un ulteriore risultato (che altri non è che una
semplice conseguenza del teorema di Rolle). Tale risultato è anche
noto in letteratura con il nome di “Teorema di Cauchy”.
Lemma 4. Se f(x) e
g(x) sono continue in [a, b] e
derivabili in (a, b) e se
g’(x) 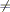 0, allora esiste un punto
0, allora esiste un punto
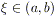 tale che
tale che
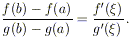
Dimostrazione. È sufficiente applicare il
teorema di Rolle alla funzione
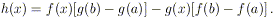
Abbiamo ora tutti gli strumenti per dimostrare il
risultato che ci interessa.
Teorema 1. Sia f(x) una funzione
periodica di periodo 2 e regolare a tratti; la serie
e regolare a tratti; la serie
di Fourier della f
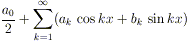
converge a f(x) nei punti in cui la f
è continua. Inoltre, in un punto x0 di
discontinuità la serie converge alla media dei limiti sinistro e
destro, cioè
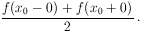
Osservazione 4. Nei punti x in cui la funzione
è continua si ha evidentemente
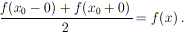
Quindi, defininendo la funzione
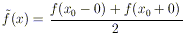
(cioè modifichiamo la f, cambiando il suo
valore nei punti di discontinuità), possiamo dire che la serie di
Fourier converge puntualmente alla funzione così definita.
Dimostrazione. Scriviamo come il solito
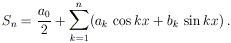
Ricordando la definizione dei coefficienti di Fourier,
abbiamo:
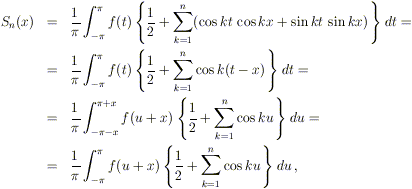
dove nel penultimo passaggio abbiamo fatto il cambio di
variabili u = t – x e nell’ultimo
abbiamo cambiato il dominio di integrazione, sfruttando la periodicità
della funzione (è indifferente su quale intervallo
[a, a + 2 ) si decida di
) si decida di
integrare).
Ricordando ora il lemma
2 si ottiene
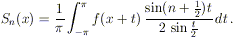
D’altra parte, tenendo conto dell’osservazione 1,
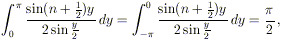
e dunque
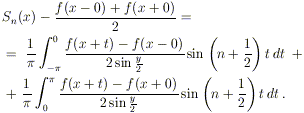
Poniamo ora
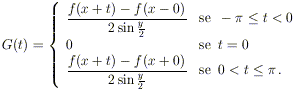
La funzione G(t) è continua in [- ,
,  ), tranne al più nei punti
), tranne al più nei punti
d – x (dove d è un punto di
discontinuità della f), nei quali ha un salto, e nell’origine.
Vediamo cosa succede quando stiamo sufficientemente vicino all’origine:
questo è infatti un punto “pericoloso” in quanto la funzione potrebbe
diventare illimitata, visto che si annulla il denominatore. Osserviamo che
prendendo |t| sufficientemente piccolo, in modo che tra t e 0
(o tra 0 e t, a seconda del segno di t) la funzione G
sia regolare (cioè non ci cadano punti di discontinuità, che
sono in numero finito), e applicando il lemma 4, si trova
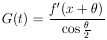
dove  è un numero (che dipende
è un numero (che dipende
da t) compreso tra t e 0 (o equivalentemente tra 0 e t).
La funzione G è allora limitata in un intorno dello 0 e dunque
in tutto l’intervallo [- ,
,  ) (altrove
) (altrove
non ci sono problemi di limitatezza). Inoltre, essendo G(t)
continua tranne che in un numero finito di punti, risulterà
integrabile. D’altra parte si ha
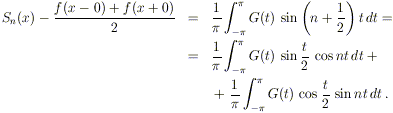
Osserviamo che le funzioni
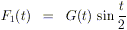 ,
, 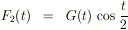
sono limitate e quindi di quadrato integrabile.
Quindi, passando al limite per n tendente all’infinito e usando
l’osservazione 2, segue immediatamente la tesi:
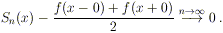
A mo’ di conclusione, voglio fornire alcuni spunti
per (eventuali) successive riflessioni o approfondimenti (che per motivi di
spazio e tempo non possono essere qui trattati in maniera dettagliata, ma di
cui la bibliografia fornita rappresenta un’ottimo riferimento).
Il risultato dimostrato
ci ha permesso di sviluppare una funzione f (periodica) come somma di
funzioni armoniche principali, che rappresentano una base per
il nostro spazio (o sistema completo). È lampante l’analogia
con quanto si fa abitualmente negli spazi vettoriali di dimensione finita:
cercare di rappresentare un vettore in termini di un sistema di riferimento
scelto come base, trovandone le coordinate rispetto a tale sistema.
Nel nostro caso, lo spazio vettoriale delle funzioni di quadrato integrabile
(che si indica a volte con L2([- ,
,  )), e che contiene chiaramente le funzioni regolari a tratti)
)), e che contiene chiaramente le funzioni regolari a tratti)
è uno spazio vettoriale di dimensione infinita (numerabile), quindi
potremmo pensare alla serie di Fourier come allo sviluppo della nostra
funzione f rispetto al sistema
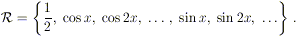
Di conseguenza, i coefficienti di Fourier possono essere
visti come le coordinate della f rispetto a tale sistema.
Il sistema 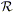 è chiamato sistema trigonometrico
è chiamato sistema trigonometrico
principale. Osserviamo che tale sistema è ortogonale
nell’intervallo [- ,
,  ) nel seguente
) nel seguente
senso: in tale intervallo l’integrale del prodotto di due qualsiasi
differenti funzioni di 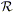 è zero,
è zero,
mentre l’integrale del quadrato di ciascuna funzione è diverso da zero
(vedi lemma 1); si parla di ortogonalità in quanto tale
integrale può essere inteso come un prodotto scalare in
L2([- ,
,  )) e quindi si
)) e quindi si
estende la nozione di ortogonalità data negli spazi di dimensione
finita.
Naturalmente, 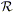 non è l’unico sistema ortogonale e
non è l’unico sistema ortogonale e
completo che si può definire in tale spazio. Quindi, lo sviluppo di
Fourier non è che un caso particolare dello sviluppo della f
rispetto ad un qualsiasi sistema ortogonale di funzioni. I risultati
dimostrati possono essere quindi riesaminati in un contesto più ampio
e interessante, che permette di comprendere meglio la “filosofia” che sta
dietro la teoria classica di Fourier.
Bibliografia:
[1] E. Giusti, Analisi matematica 2,
Bollati-Boringhieri (1983)
[2] W. Rudin, Analisi reale e complessa,
Bollati-Boringhieri (1974)
[3] A. N. Kolmogorov, S. V. Fomin,
Elementi di teoria delle funzioni e di analisi funzionale, Edizioni
Mir (1980)
Impaginato da Gino Favero