E’ vero che la forza esercitata dal Sole sulla Luna è 2,2 volte quella esercitata dalla Terra, ma questo NON significa che si debba ritenere il nostro satellite slegato dalla Terra e orbitante attorno al Sole come un pianeta.
Questa era la tesi esposta dal noto scrittore di fantascienza e divulgatore scientifico Isaac Asimov nel saggio Mooning around, pubblicato nel suo libro Of Time and Space and Other Things del 1965.
Seguiamo il suo ragionamento: se consideriamo il rapporto tra le masse del Sole (M) e della Terra (m) e il rapporto tra le distanze della Luna dal Sole (R) e dalla Terra (r) e confrontiamo le espressioni della forza gravitazionale, abbiamo che:
.gif)
Se andiamo ad applicare l’equazione precedente a tutti i satelliti del sistema solare, vediamo che in pratica il satellite in assoluto sentirà maggiormente la forza del Sole se la sua distanza supererà un certo valore, che si può scrivere nel modo seguente:
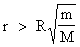
La seguente tabella mostra un fatto singolare: la Luna è l’unico satellite che si trova oltre questa distanza.
| Pianeta | 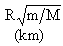 |
distanza del satellite più lontano (km) |
satellite più lontano |
mpianeta / msatellite |
| Mercurio | 23.701 | – | – | – |
| Venere | 170.039 | – | – | – |
| Terra | 260.627 | 384.500 | Luna | 81 |
| Marte | 130.080 | 23.500 | Deimos | 426.666.666 |
| Giove | 24.146.492 | 24.060.000 | Sinope | 13.350 |
| Saturno | 24.231.618 | 12.954.000 | Phoebe | 43.850 |
| Urano | 19.095.143 | 587.000 | Oberon | 24.860 |
| Nettuno | 32.490.975 | 5.600.000 | Nereide | 4.761 |
Tuttavia il fatto indiscutibile che la forza che il Sole esercita sulla Luna è 2.2 volte quella che la Terra esercita sulla Luna non autorizza a concludere che la Luna non sia legata alla Terra!
Infatti nell’interazione tra la Terra e la Luna l’effetto della presenza del Sole può essere considerato trascurabile.
Per essere più precisi, l’influenza del Sole si manifesta come una perturbazione con un valore di accelerazione massimo di circa 1/90 circa dell’attrazione terrestre, come viene spiegato in questa dispensa.
Una spiegazione qualitativa di ciò (e di conseguenza del fatto che sebbene l’attrazione del Sole sulla Luna sia più forte di quella esercitata dalla Terra, la Luna rimane saldamente legata gravitazionalmente al nostro pianeta) può essere la seguente.
E’ vero che il Sole attrae a sé la Luna più di quanto non riesca a fare il nostro pianeta; ma il Sole attrae a sé anche la Terra, con il risultato che in questo balletto cosmico a tre la Luna non si allontana mai dalla Terra, tanto da poterle sfuggire. Più quantitativamente si può dire l’accelerazione a’ con cui il Sole attrae la Luna, cioè:
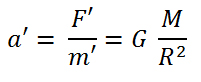
(dove F’ è la forza con cui il Sole attrae la Luna, di massa m‘, e G è la costante di gravitazione universale) è molto vicina a quella a con cui il Sole attrae la Terra, pari a:
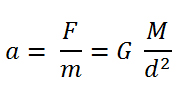
(dove stavolta F è la forza che il Sole esercita sulla Terra e d è la distanza Sole-Terra). Siccome le differenze tra le due distanze Sole-Luna e Sole-Terra (dovute all’orbita della Luna intorno alla Terra) sono molto piccole, in prima approssimazione possono essere trascurate e quindi si può affermare che il Sole, imprimendo di fatto la stessa accelerazione alla Terra ed alla Luna, ha un effetto trascurabile (solo una perturbazione, appunto) nell’interazione tra questi due corpi. In altre parole il moto della Terra e della Luna intorno al loro comune centro di massa avviene in buona sostanza come se il Sole non esistesse!
Ciò spiega l’apparente paradosso di una Luna che, pur essendo attratta più dal Sole che dalla Terra, risulta saldamente legata gravitazionalmente al nostro pianeta.
D’altra parte non è un caso che il parametro che misura l’ampiezza della zona dell’influenza gravitazionale di un pianeta non è il raggio r definito da Asimov (che risulta inadatto a misurare quanto un satellite sia legato al suo primario), ma il cosiddetto raggio di Hill, che viene valutato proprio tenendo in considerazione la doppia azione del Sole sul satellite e sul pianeta e che risulta definito approssimativamente come:
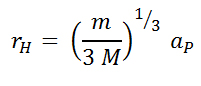
(vedi https://it.wikipedia.org/wiki/Sfera_di_Hill), dove aP è il semiasse maggiore dell’orbita del pianeta intorno al Sole, m è la massa del pianeta ed M quella del Sole. In altre parole il raggio di Hill definisce una regione di spazio, detta sfera di Hill o sfera di influenza, all’interno della quale il campo gravitazionale del pianeta domina su quello del Sole.
Se si valuta il rapporto as/rH tra il semiasse maggiore dell’orbita del satellite ed il raggio di Hill del pianeta, si vede che esso vale per la Luna 0.259, il che indica quantitativamente che la Luna è ben dentro la regione di influenza gravitazionale della Terra. D’altra parte nel Sistema Solare sono noti almeno 22 satelliti che hanno un valore di as/rH maggiore di quello lunare (Altieri, 2002) e che pertanto risultano legati al loro primario meno (in genere molto meno) di quanto la Luna non lo sia alla Terra.
Bibliografia
Altieri F., Derivazione del Raggio di Hill e confronto con i dati osservativi, Dissertazione finale del corso di Elementi di Planetologia, Dottorato di Ricerca in Fisica (XVII Ciclo), Università degli Studi di Lecce (2002).