Se si parla di statistiche sull'altezza del Sole viene in mente la classica domanda sul valore medio, utile ad esempio per inclinare correttamente i pannelli solari. Dato che nel corso dell'anno l'altezza del Sole oscilla attorno all'equatore celeste, in tal caso la risposta sarebbe pari all'inclinazione dell'equatore celeste nel punto della Terra considerato. Per l'Italia tale valore è prossimo ai 45 gradi.
La domanda posta dal lettore però è più insidiosa perché parla di valore più probabile. In altre parole, il lettore ci chiede quale sarebbe l'altezza più "gettonata" in un campione casuale di osservazioni del Sole.
Partiamo da un caso specifico e cioè l'altezza del Sole al meridiano.
Sappiamo tutti che il Sole oscilla tra due estremi corrispondenti ai solstizi, con andamento approssimativamente sinusoidale. È intuitivo quindi che la nostra stella si troverà più spesso agli estremi perché la velocità con cui varia la sua declinazione è massima agli equinozi e poi va diminuendo sempre di più fino ad annullarsi. Del resto il termine latino sol stitium deriva proprio da questo fatto!
Matematicamente si può calcolare la densità di probabilità della sinusoide, nel modo ottimamente illustrato nel blog di Atif, e vediamo che in effetti ha due picchi molto pronunciati in corrispondenza degli estremi.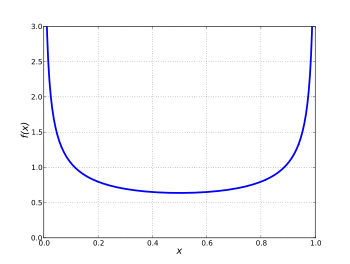
Insomma, se volessimo prendere la tintarella con il Sole solo al meridiano, la sedia a sdraio dovrebbe avere solo due posizioni. Una per il solstizio d'estate e una per quello d'inverno 😉
Scherzi a parte, il problema più generale di determinare il valore più probabile dell'altezza del Sole in tutto il cielo è un esercizio interessante anche se condotto in modo intuitivo e non tramite equazioni.
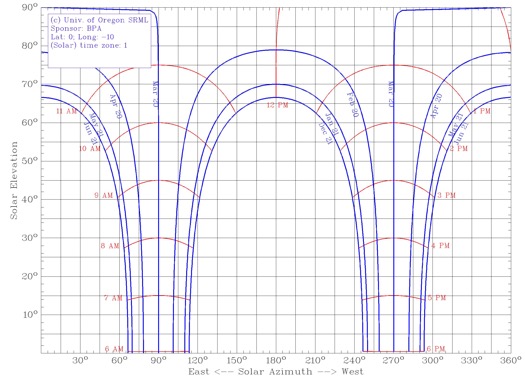
Ci aiuteremo quindi con dei grafici ottenuti dal Solar Radiation Monitoring Laboratory dell'Università dell'Oregon: mostrano la fascia del cielo entro la quale si vede muoversi il Sole per diverse latitudini, in proiezione ortografica. Per valutare l'altezza più probabile dovremo sì valutare l'estensione verticale della fascia, ma anche fare uno sforzo di immaginazione: pensare che il Sole in questa fascia oscillerà durante l'anno in modo sinusoidale.
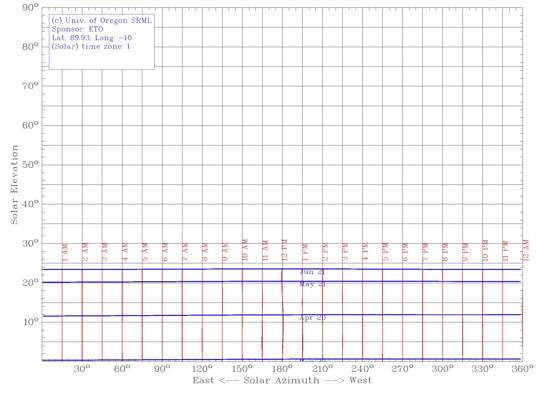
Partiamo dal Polo perché ci permette di ricollegarci direttamente al caso particolare che abbiamo trattato poc'anzi. Ai poli il cammino del Sole è parallelo all'orizzonte e la densità di probabilità della sua altezza quindi è molto ben approssimata dal grafico visto in precedenza. Nel grafico della densità di probabilità dell’altezza del Sole avremo allora un bel picco pronunciato in corrispondenza di 23.5 gradi (l'altro picco è sotto l'orizzonte, alla stessa altezza, stavolta negativa).
Scendendo di latitudine, la fascia del percorso del Sole contemporaneamente si alza e si deforma piegando le estremità verso il basso. Quindi il valore più probabile scende.
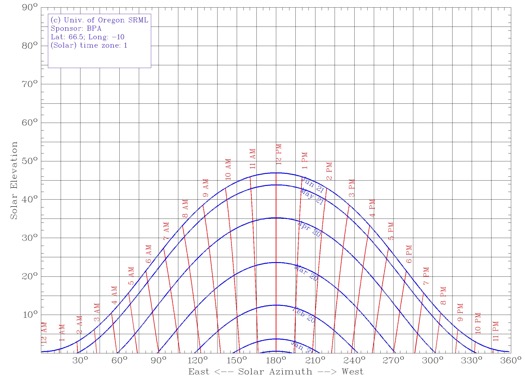
Infatti al circolo polare è evidente che il valore più probabile sia prossimo a zero. Il fatto che il Sole stazioni verso l'alto nella fascia è ampiamente compensato dalla piegatura, che rende sempre più esiguo il contributo della parte alta della curva, a vantaggio della zona dove la curva è più larga (e dove il Sole passa più tempo).
Stranamente quindi, ai circoli polari i pannelli solari dovrebbero essere … perpendicolari al terreno!
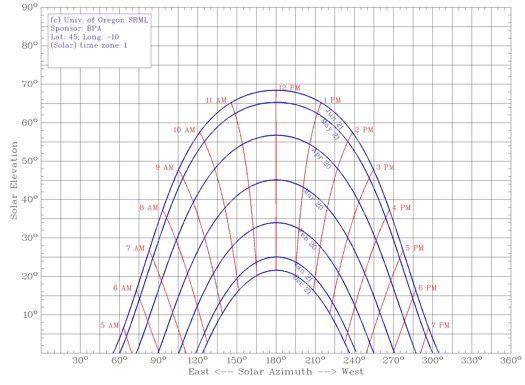
Alle nostre latitudini la fascia percorsa dal Sole nel cielo è ben staccata dall'orizzonte ma anche ben piegata agli estremi e dunque il valore più probabile sarà maggiore di zero, ma prossimo all'altezza del Sole al solstizio d'inverno, vicino alla zona dove la fascia è più larga!
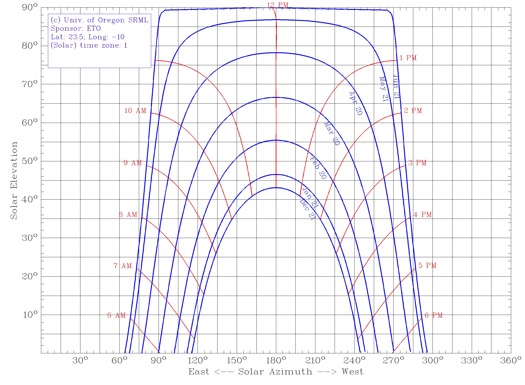
Ai tropici il Sole riesce a toccare per un momento lo zenith, ma l'altezza più probabile si concentra nuovamente al solstizio d'inverno. Idem per l'equatore.
Certo, lavorare di fantasia su questi grafici fa venire un po' di mal di testa….
Per fortuna ci viene in soccorso l'informatica: possiamo simulare quel che ci chiede il lettore scrivendo un programma che faccia davvero la statistica dell'altezza del Sole in vari punti del globo.
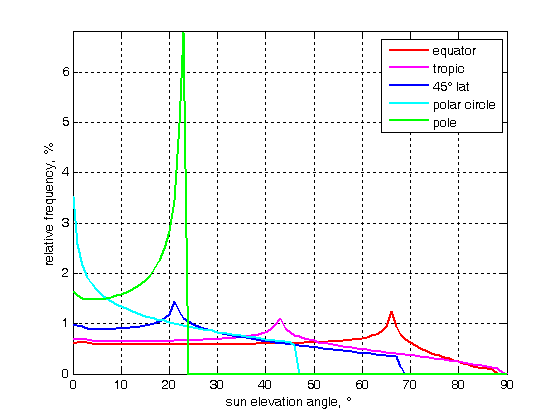
Ringrazio Federico Angelini per aver preparato i seguenti grafici.
Queste tracce dimostrano ciò che avevamo intuito esaminando le cinque condizioni precedenti.
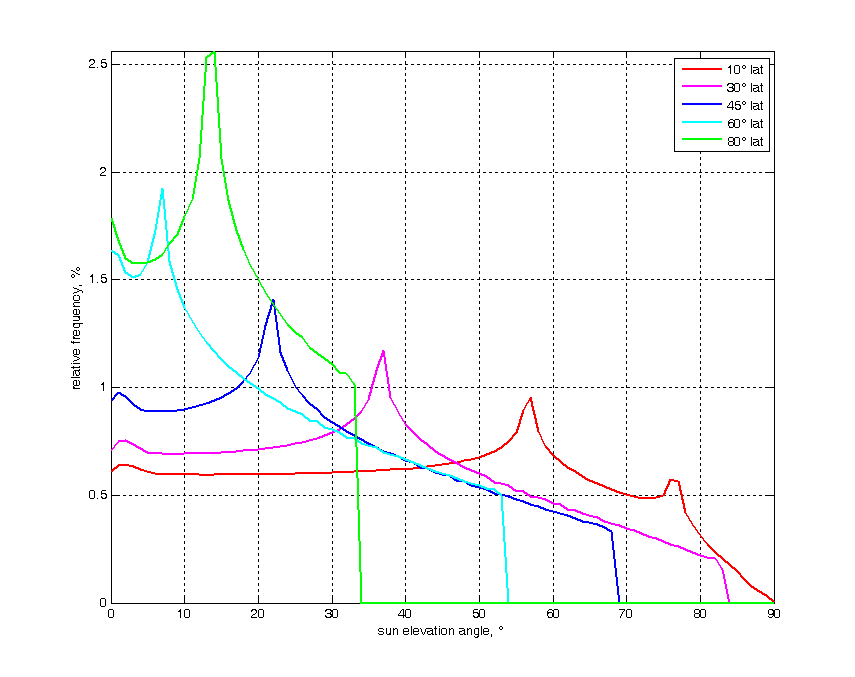
Il grafico seguente mostra la stessa statistica ma per altre latitudini.
 Per chiudere con un sorriso, questo esercizio dimostra che guidare con gli occhiali da Sole non serve soltanto per darsi un tono… alle nostre latitudini infatti abbiamo visto che è molto probabile trovare il Sole alto solo una ventina di gradi sull'orizzonte!
Per chiudere con un sorriso, questo esercizio dimostra che guidare con gli occhiali da Sole non serve soltanto per darsi un tono… alle nostre latitudini infatti abbiamo visto che è molto probabile trovare il Sole alto solo una ventina di gradi sull'orizzonte!