Per trovare le coordinate equatoriali celesti di un astro,tra le altre cose ho bisogno di sapere l’angolo formato dal meridiano passante per l’astro e il meridiano passante per il punto gamma. Domanda: come faccio a sapere dalla mia posizione geografica con data e ora dove si trova in quel momento il punto gamma ?

L'angolo formato dal meridiano passante per l'astro e quello passante per il punto gamma (punto $gamma$ o punto d'Ariete, o anche punto vernale, o ancora nodo ascendente) è proprio una delle due coordinate equatoriali, che prende il nome di ascensione retta (indicata con la sigla RA dall'inglese Right Ascension o, sui testi italiani, con AR, in figura indicata con la lettera $alpha$ ). L'altra è la declinazione (in figura $delta$ ), ovvero la distanza angolare dell'oggetto dall'equatore celeste.

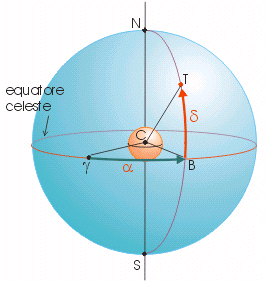
Il punto $gamma$ è uno dei due punti in cui l'equatore celeste interseca l'eclittica, l'altro prende il nome di punto omega $Omega$ (o punto di bilancia, o nodo discendente). Il punto $gamma$ , nel sistema equatoriale, è proprio l'origine delle coordinate, quindi ha coordinate nulle (la Declinazione è 0°, trovandosi il punto sull'equatore celeste, l'Ascensione Retta è 0^h00^m 00^s per definizione, essendo questa misura presa proprio a partire dal punto $gamma$ ). Le coordinate di un punto del cielo, ad esempio quello occupato da una stella, in questo sistema, rimangono quasi sempre le stesse, e il sistema è detto uranografico.
La parola quasi fa riferimento al fatto che, in realtà, anche il punto $gamma$ non è fisso, a causa della precessione degli equinozi e di altri moti del nostro pianeta cosiddetti secolari, per questo le coordinate, in particolare l'ascensione retta, vengono riferite a un tempo ben preciso. Oggi molti planetari virtuali (come ad esempio Stellarium) aggiornano in tempo reale il valore dell'ascensione retta.

Quindi la data, a cui fa riferimento la domanda, serve proprio a conoscere esattamente dove si trova il punto $gamma$ e calcolarne in modo esatto la posizione.

Se ho un telescopio con sistema equatoriale, non devo fare altro. Una volta orientato il telescopio, il punto $gamma$ si troverà sempre nell'origine del sistema di riferimento sferico, ovvero in corrispondenza dello 0 di entrambe le coordinate.

Se voglio trovare la posizione del punto $gamma$ rispetto alla mia posizione, devo ricorrere però ad un altro sistema di coordinate, chiamate orizzontali (o alt-azimutali). Questo sistema è centrato sull'osservatore ed ha come cerchio di riferimento non l'equatore ma l'orizzonte (da qui il nome del sistema di coordinate) e la semicirconferenza perpendicolare all'orizzonte (cioè verticale) e passante per il Nord. Questo sistema dipende dal punto in cui mi trovo e dal momento in cui effettuo l'osservazione, pertanto si tratta di un sistema locale. Le coordinate prendono il nome di altezza (rispetto all'orizzonte), in figura h, e azimut, in figura A. Nella figura l'osservatore si trova nel punto O e i punti cardinali sono presi sull'orizzonte.

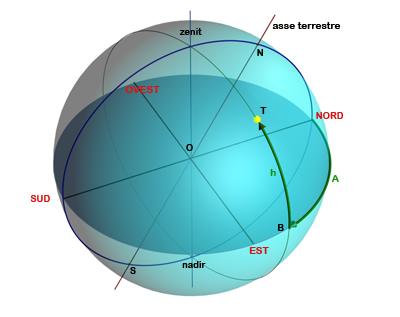
Quindi la domanda possiamo riformularla così: quali sono, in un certo istante, l'altezza e l'azimut del punto $gamma$ , conoscendo la mia posizione geografica, ovvero la latitudine ( $varphi$ ) e la longitudine ( $lambda$ ) della mia posizione, la data e l'ora dell'osservazione?

Per rispondere alla domanda si tratta di conoscere sostanzialmente qual è il modo di passare da un sistema all'altro, ovvero la posizione dell'origine del sistema di coordinate equatoriali nel sistema orizzontale, visto che il punto $gamma$ è l'origine delle coordinate equatoriali.

Si tratta di due sistemi di coordinate sferiche, in cui, pur rimanendo sulla stessa superficie sferica, cambiano i cerchi e i punti di riferimento. Inoltre i due sistemi sono in moto l'uno rispetto all'altro (la posizione di un osservatore sulla superficie terrestre cambia continuamente rispetto alla posizione del punto $gamma$ ). Nella tabella sono sintetizzati alcune caratteristiche e nomenclatura dei due sistemi di coordinate, qui se ne trova una più dettagliata.

	Sistema equatoriale	Sistema orizzontale
Asse di riferimento	Asse polare celeste	Verticale dell'osservatore
Poli	Polo Nord e Sud	Zenit e Nadir
Cerchio fondamentale	Equatore celeste	Orizzonte
Semicerchio origine	Verticale Nord	Coluro degli equinozi
Origine	Punto cardinale Nord	Punto $gamma$
Coordinate	ascensione retta ( $alpha$ ) declinazione ( $delta$ )	azimut ( $A$ ) altezza ( $h$ )

Per passare da un sistema all'altro occorre utilizzare la trigonometria sferica.

Tralasciando i calcoli, le formule per il passaggio dalle coordinate equatoriali a quelle orizzontali sono

$A = arctan left (frac{sin au}{cos au cdot sin varphi – an delta cdot cos varphi} ight )$ e $h = arcsin left ( sin varphi cdot sin delta + cos varphi cdot cos delta cdot cos au ight )$

Ai simboli noti, cioè alla declinazione $delta$ e alla latitudine $varphi$ , si è aggiunta la quantità $au$ che prende il nome di angolo orario e si calcola sottraendo al Tempo Siderale Locale l'ascensione retta $alpha$ .
Il Tempo Siderale Locale (TSL) è l'ora del tempo siderale del punto da cui si fa l'osservazione, e si può calcolare sottraendo al tempo siderale di Greenwich la longitudine del punto di osservazione. Esso indica anche l'ascensione retta dei punti che, in ogni istante, stanno attraversando il meridiano del punto di osservazione.

Nel nostro caso, considerando che $alpha = delta = 0$ le formule si riducono a

$A = arctan left ( frac{sin ext{TSL}} {cos ext{TSL} cdot sin varphi} ight )$ e $H = arcsin left ( cos varphi cdot cos ext{TSL} ight )$

Per cui è possibile, istante per istante, conoscendo il Tempo Siderale Locale (che contiene informazioni su data, ora e longitudine) e la latitudine, conoscere la posizione del punto $gamma$ .

Altre pagine di ViaLattea che parlano di questo argomento sono:

Bibliografia:

le figure sono prese da Eratostene