La sua perplessità è giusta e deriva dalla divulgazione frettolosa dei concetti relativistici di contrazione delle lunghezze e del suo duale, ovvero la dilatazione temporale.
È troppo facile (e sbagliato) raccontare le meraviglie della relatività come se fosse un effetto … psichedelico "il tempo rallenta fino a fermarsi quando si raggiunge la velocità della luce". Oppure dire che "un'asta si accorcia" sempre più man mano che la sua velocità aumenta.
Se prendiamo la definizione del principio di relatività, che è un pilastro della fisica, ci accorgiamo subito che le cose non possono stare come vengono raccontate comunemente.
Esso recita: "le leggi della fisica sono le stesse in tutti i sistemi di riferimento".
Esso recita: "le leggi della fisica sono le stesse in tutti i sistemi di riferimento".
Di conseguenza, come lei intuisce correttamente, non può esistere una strana forza che rallenta le lancette dell'orologio quando l'astronave viaggia a velocità relativistiche o una forza ancora più strana che la schiaccia nella direzione del moto.
A bordo dell'astronave non c'è nulla che possa indicare che la sua velocità è altissima. O addirittura che sia ferma. La fisica è la stessa.
E poi l'intuito ci fa sorgere un dubbio: se il moto è relativo, allora ciascuno vede l'altro in movimento, ma quindi questo accorciamento chi riguarda realmente? E allora ecco sorgere tutta una serie di paradossi, ad esempio quello dello sciatore relativistico che si trova davanti una buca grande esattamente quanto gli sci. Si accorciano gli sci e quindi lui cadrà nella buca, o si accorcia la buca e lo sciatore passerà tranquillamente?
Preferisco spiegare la contrazione delle lunghezze con un esempio: prendiamo due porte una di fronte all'altra, parallele. Ciascuna vede l'altra in tutta la sua lunghezza. Ora apriamo di 60 gradi una delle porte. Essa apparirà dimezzata per effetto della proiezione sul piano dell'altra. Tuttavia anche la seconda porta apparirà dimezzata rispetto alla prima. La situazione è simmetrica e in realtà nessuna delle due ha subito alcuna modificazione!
È come se – inclinandosi – ciascuna delle due porte fosse andata parzialmente in un'altra dimensione, mantenendosi inalterata in se' ma apparendo dimezzata all'altra.
Ed in effetti quando parliamo di relatività dobbiamo tenere presente che lo scenario in cui ambientiamo i nostri ragionamenti deve essere lo spaziotempo e non semplicemente lo spazio E il tempo. Stiamo parlando quella mirabile mescolanza dello spazio e del tempo, che a noi umani paiono entità totalmente diverse. È infatti nello spaziotempo che i paradossi che abbiamo citato trovano soluzione (si veda ad esempio questa risposta: http://www.vialattea.net/esperti/php/risposta.php?num=725)
Certo, per entrare nella logica dello spaziotempo dobbiamo rinunciare alle nostre nozioni comuni di spazio, di tempo, di simultaneità. Ma veniamo ben ripagati!
Ma se abbiamo detto che la contrazione/dilatazione è un effetto illusorio, allora il paradosso dei gemelli si verificherebbe davvero oppure no?
Vediamolo: due gemelli, semplificando la questione, nascono nello stesso istante. Usando un linguaggio molto da fisici e molto poco da poeti, possiamo immaginarli come due orologi che partono allo stesso momento e nello stesso luogo. Uno dei due sale su un'astronave e viaggia per anni a velocità relativistiche. Quando si incontrano di nuovo, i gemelli scoprono di avere età diverse!
La spiegazione però non può chiamare in causa fenomeni prodigiosi (al gemello viaggiante la barba cresce più lentamente, le sue cellule hanno un metabolismo rallentato, ecc.) perché sarebbe una violazione del principio di relatività.Niente affatto: a bordo dell'astronave la vita scorre normalmente!
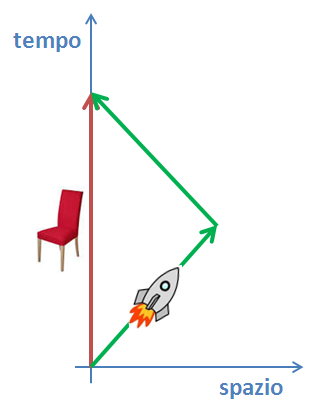
Per risolvere l'aspetto paradossale dobbiamo – come detto prima – inquadrare il problema nella cornice adatta: lo spaziotempo. In questo modo diventa chiaro chei due gemelli compiono due cammini diversi nello spaziotempo. Allora la faccenda diventa persino banale: due persone partono da A e arrivano a B prendono strade diverse, perché stupirsi se, quando si ritrovano, uno dei due ha le suole più consumate dell'altro?
Per risolvere l'aspetto paradossale dobbiamo – come detto prima – inquadrare il problema nella cornice adatta: lo spaziotempo. In questo modo diventa chiaro chei due gemelli compiono due cammini diversi nello spaziotempo. Allora la faccenda diventa persino banale: due persone partono da A e arrivano a B prendono strade diverse, perché stupirsi se, quando si ritrovano, uno dei due ha le suole più consumate dell'altro?
|
Grazie della spiegazione con l’esempio dei gemelli. Ma se nel caso dei gemelli ci fosse solo il gemello sull’astronave e il gemello sulla sedia senza altro riferimento, come fa a saper il gemello sull’astronave che è lui che si muove? Potrebbe essere benissimo il gemello sulla sedia che si muove. E quindi all’incontro dovrebbe essere il gemello più giovane
anche senza riferimenti esterni, la situazione dal punto di vista fisico è ben definita perché il gemello che acquista velocità subisce una accelerazione, l’altro no