Consideriamo una funzione
f : I –> 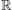
(dove I è un intervallo di 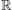 )
)
e supponiamo che tale funzione sia sufficientemente regolare (ad esempio
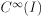 , in modo che abbia senso parlare di derivata di ogni
, in modo che abbia senso parlare di derivata di ogni
ordine; in realtà per rispondere alla domanda fatta sarebbe
sufficiente limitarci a considerare il caso 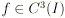 ).
).
Ovviamente possiamo
guardare il grafico di tale funzione come una curva piana di equazioni
parametriche:
a : I –> 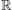 2
2
a : x –> a(x) := (x, f(x));
per tale curva ha senso parlare di retta tangente, curvatura
e cerchio osculatore. Vediamo di riferire tali concetti alla
funzione f.
-
Retta tangente: il vettore tangente
alla curva nel punto a(x0) (con
x0 I) è dato dal vettore derivata prima:
I) è dato dal vettore derivata prima:
a’(x0) = (1, f(x0));
chiaramente il modulo di questo vettore non è
necessariamente 1, cioè la curva non è necessariamente
parametrizzata a velocità 1 (per le curve a velocità
1 le formule per la curvatura sono particolarmente semplici; purtroppo
nel caso di curve parametrizzate in questo modo, la parametrizzazione a
velocità 1 corrisponde al caso (troppo) particolare
f’(x) = 0, cioè alla retta
f(x) = c). Quindi, la retta tangente
alla curva nel punto a(x0) è data da:r:
y – f(x0) = f’(x0) (x – x0).
(x – x0).Quindi effettivamene la derivata prima in
x0 rappresenta una misura dell’inclinazione della
funzione f(x), in quanto è il coefficiente angolare
della retta tangente alla curva nel punto a(x0)
(la retta tangente è la retta che meglio approssima la curva in
un piccolo intorno del punto). -
Curvatura: Supponiamo che, nel passare dal
punto M al punto M’ di una curva a, la tangente
ruoti di un angolo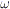 (espresso in radianti); il
(espresso in radianti); il
rapporto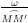 fra l’angolo
fra l’angolo 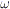 e la lunghezza dell’arco MM’, che caratterizza
e la lunghezza dell’arco MM’, che caratterizza
quanto si “incurva” la curva nel tratto MM’, si chiama curvatura
media dell’arco MM’ (osserviamo che la curvatura media di
ogni arco di circonferenza di raggio R è uguale a
1 / R).
Si definisce curvatura della curva a nel punto M
il limite a cui tende la curvatura media dell’arco MM’ quando il
punto M’ tende a M: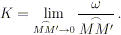
La curvatura caratterizza quanto si incurva la linea nel
punto considerato. La curvatura di una retta è ovunque nulla.
La curvatura di una circonferenza di raggio R è
1 / R.
Nel caso della nostra curva a (espressa come grafico della
funzione f) possiamo esprimere la curvatura in termini della
funzione f e delle sue derivate. Si dimostra (per la
dimostrazione rimandiamo ad un qualsiasi testo di geometria
differenziale) che nel nostro caso: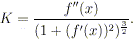
Quindi non è vero in generale che la derivata
seconda rappresenta la curvatura; quello che è vero è che
il suo segno è uguale al segno della curvatura (infatti il segno
della derivata seconda ci permette di determinare la convessità
o la concavità della funzione). È questo l’errore
fondamentale presente nel ragionamento – in sé acuto e
interessante – dell’autore della domanda: la derivata seconda
contribuisce al calcolo della curvatura, ma non rappresenta la curvatura!
(Osserviamo che il caso in cui K = f”(x)
è il caso in cui f’(x) = 0, cioè in
corrispondenza di un punto critico per la funzione).
Del resto un lettore attento noterebbe immediatamente che “qualcosa non
funziona” nel ragionamento esposto nella domanda. Consideriamo la parabola
y = x2: tale parabola ha derivata seconda
costante, ma lo stesso non si può dire della sua curvatura. Oppure
prendiamo in esame la semicirconferenza y =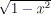 (per -1
(per -1 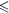 x
x 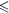 1): questa ha curvatura costante (per quanto abbiamo
1): questa ha curvatura costante (per quanto abbiamo
detto in precedenza sulla curvatura di una circonferenza), ma la derivata
seconda della funzione f(x) =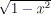
si guarda bene dall’essere ovunque costante! -
Cerchio osculatore: Consideriamo un punto
a(x), in cui la curvatura è K(x)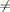 0. Possiamo considerare una circonferenza tangente
0. Possiamo considerare una circonferenza tangente
alla curva in tale punto e con la stessa curvatura. Per quanto abbiamo
detto prima, il raggio di tale circonferenza dovrà essereR = 1 / K(x)
che viene detto raggio di curvatura. Il centro
di tale circonferenza è dato da:c(x) = a(x) + Rn(x)
dove n(x) è il versore normale
alla curva nel punto a(x). Tale cerchio prende il nome di
cerchio osculatore o cerchio di curvatura.
NOTA: La curva c(x) al variare di x I (ovviamente per i punti in cui la curvatura
I (ovviamente per i punti in cui la curvatura
non è nulla) prende il nome di evoluta della curva a.
Dopo aver introdotto questi concetti fondamentali nello
studio di una curva piana ed il loro legame con la funzione f
(giustificando e confutando alcune tesi proposte), vorremmo passare ad
analizzare il ruolo delle derivate di ordine superiore della f (in
particolare della derivata terza). La cosa non è semplice e immediata
come potrebbe sembrare.
Osserviamo che la
variazione della curvatura genera una variazione del centro di curvatura e
quindi costituisce la forza generatrice della curva evoluta. In un
certo senso quindi la derivata della curvatura può essere collegata a
quello che il lettore definisce “l’indice puntuale di decentramento della
f(x)”, ossia la variazione del centro di curvatura della
f(x) (una sorta di “eccentricità”). Il calcolo di tale
derivata (in termini della f) include certamente la derivata terza
della f, ma non solo. Infatti, in tale espressione compariranno anche
la derivata prima, la derivata seconda e la funzione stessa (legate tra loro
da un’espressione algebrica più o meno complessa, che mi esimo dal
calcolare); quindi non è possibile legare direttamente la derivata
terza con una proprietà geometrica puntuale della curva in esame: la
derivata terza collabora al calcolo di tale indice, ma non è il solo
fattore. Stesso ragionamento per le derivate d’ordine superiore.
Tanto per chiarire
quanto appena detto (o meglio: per convincervi della validità della
mia obiezione) consideriamo sempre il caso di una parabola. In questo caso
la derivata terza è ovunque nulla, ma la curva ha un decentramento
continuo (cioè la sua curva evoluta non è un singolo
punto!), in quanto la curvatura non è identicamente costante. Potremmo
fare la stessa obiezione anche considerando la semicirconferenza: in questo
caso l’indice di decentramento dovrebbe essere ovunque nullo… ma la
derivata terza della funzione f(x) = 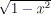 non è ovunque nulla!
non è ovunque nulla!
A mo’ di conclusione
voglio accennare una mia idea su quella che può essere una vera
interpretazione geometrica di tali derivate (o meglio, un altro punto di
partenza da cui affrontare il problema proposto). Uno dei risultati
fondamentali (quanto meno a mio parere) dell’analisi moderna è dovuto
Brook Taylor (1685-1731) ed afferma quanto segue:
Teorema. Sia f(x) una funzione di
classe Cn in un intorno del punto x0; allora si
ha:
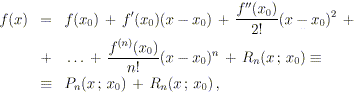
dove
Rn(x, x0) è una
“funzione resto” che soddisfa
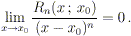
In altre parole, riusciamo ad approssimare (in un intorno di
x0) la funzione f in termini di un polinomio di
grado n (quello che sopra abbiamo chiamato
Pn(x, x0)) e l’errore
commesso Rn(x, x0) è
“sufficientemente piccolo”.
Quindi le derivate
calcolate nel punto x0 altro non sono (a meno del fattore
moltiplicativo 1 / n!, che non dipende dalla funzione ma
solo dall’ordine di derivazione) che i coefficienti delle curve polinomiali
che meglio approssimano la funzione in un intorno del punto. Ad esempio, per
n = 1 otteniamo che la migliore retta che approssima la
funzione in tale punto è la retta
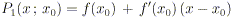
che altri non è che la retta tangente alla curva nel
punto. Osserviamo che la pendenza della funzione si ricava proprio
dal coefficiente angolare della retta tangente, cioè
f’(x0).
Vediamo che cosa succede
per n = 2. Troviamo che la parabola che meglio approssima la
funzione in un intorno del punto è
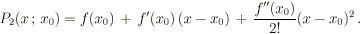
Da tale parabola approssimante, si possono dedurre alcune
proprietà geometriche puntuali della curva, quali ad esempio la
curvatura; infatti la curvatura della parabola nel vertice è data
da
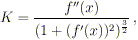
che è proprio l’espressione trovata per la curvatura.
Quindi, vedendo il
problema da un altro punto di vista, possiamo concludere che le derivate non
sono legate direttamente alle proprietà geometriche della
nostra funzione (vista come curva piana) ma rappresentano i coefficienti
delle funzioni polinomiali che meglio rispecchiano il comportamento della
funzione in un intorno del punto; è proprio da questi polinomi (e
quindi indirettamente dalle derivate, che infatti compaiono in tali
espressioni in maniera più o meno complessa) che possiamo ricavare
informazioni su tale geometria locale (inclinazione, curvatura,
“decentramento”, etc…).
Per concludere vorrei segnalare alcuni testi
attraverso i quali è possibile approfondire quanto ho fin qui discusso
(naturalmente non sono gli unici, né i migliori, ma semplicemente
quelli a mia conoscenza):
[1] E. Sernesi, Geometria 2,
Bollati-Boringhieri, Torino 1994.
[2] A. Gray, Modern differential geometry of
curves and surfaces, CRC press, Boca Raton, Florida 1993.
[3] M. Do Carmo, Differential geometry of
curves and surfaces, Prentice Hall, New Jersey 1976.
[4] R. Courant, H. Robbins, Che
cos’è la matematica?, Bollati-Boringhieri, Torino 1971.
Si veda inoltre una precedente risposta di Carlo Consoli sullo stesso argomento.
Impaginato da Gino Favero