Il Principio di Cavalieri è una delle proposizioni fondamentali della Geometria pre-Analisi, in quanto è alla base della dimostrazione di buona parte delle formule di calcolo dell’area e del volume. Esso è sostanzialmente composto da due affermazioni, una valida per la geometria piana e l’altro per quella solida e afferma che
"Considerate due figure piane di uguale altezza e un fascio continuo di rette tutte perpendicolari all’altezza comune, se le sezioni delle due figure piane ottenute dalla stessa retta hanno sempre lunghezza uguale allora le due figure piane hanno area uguale."
"Considerati due solidi di uguale altezza e un fascio continuo di piani tutti perpendicolari all’altezza comune, se le sezioni dei due solidi ottenute dallo stesso piano hanno sempre area uguale allora i due solidi hanno volume uguale."
Unito con il Teorema di Talete, rispettivamente a due e tre dimensioni, il Principio di Cavalieri permette di affermare che se le sezioni non sono equivalenti ma hanno tutte le stesso rapporto allora lo stesso rapporto ci sarà anche tra le aree o i volumi.
Cavalieri ha formulato il principio senza fornirne una dimostrazione rigorosa perché all’epoca non era ancora disponibile l’analisi matematica, in particolare il calcolo integrale. Per tale motivo tale proposizione è nota come principio e non come teorema, ma il suo uso si è rivelato indispensabile, nei secoli antecedenti costruzione dell’analisi, per l’ottenimento delle formule di aree e soprattutto dei volumi delle più disparate figure. Pertanto, anche in consideraziome dei ragionamenti intuitivi che possono portare a questo risultato, è stato considerato una delle proprietà fondamentali del volume e dell’area fino a che il calcolo integrale non lo ha reso obsoleto. Tuttavia va notato che Cavalieri, nel fornire degli argomenti a sostegno del suo Principio, ha anticipato molte idee che saranno successivamente formalizzate in maniera rigorosa dal calcolo integrale.
La dimostrazione più rigorosa che si può dare di tale Principio richiede l’uso degli integrali, il che rende inutile il principio stesso perché gli integrali permettono di calcolare direttamente l’area e il volume di un insieme di figure molto più vasto di quello che può essere analizzato solo mediante il Principio di Cavalieri e i risultati della geometria deduttiva. È comunque interessante percorrerla per notare poi le analogie con un altra dimostrazione, meno rigorosa ma più intuitiva, che vedremo successivamente.
Consideriamo due figure piane F1 e F2. Le loro aree sono, per definizione, date dagli integrali
![]()
Se le due figure hanno la stessa altezza, come deve essere per ipotesi, allora possiamo traslare e/o ruotare rigidamente una delle due figure affiancandole in modo che gli estremi inferiore e superiore della variabile y siano gli stessi per i due integrali. In corrispondenza di ogni valore di y la variabile x avrà degli estremi di integrazione che dipenderanno da y

che con un passaggio immediato diventano
![]()
le parentesi quadre rappresentano la lunghezza della corda che viene intercettata da una retta orizzontale di ordinata y quando interseca rispettivamente la figura F1 e la figura F2. La situazione descritta può essere visualizzata nella seguente figura in cui sono presenti tre quadrilateri, di cui uno mistilineo, di uguale altezza ed equivalenti.
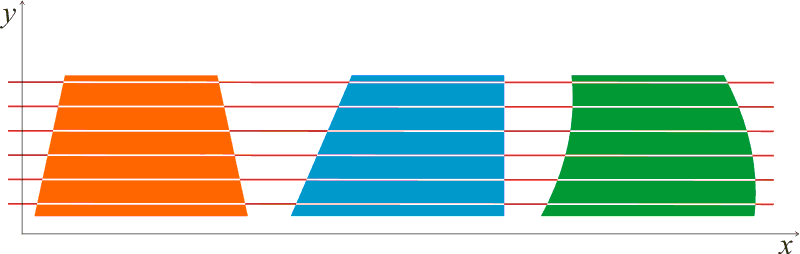
Se tali corde hanno la stessa lunghezza, come richiede il Principio di Cavalieri a 2-D, allora gli integrandi degli integrali in dy sono uguali per ogni y e quindi sono uguali anche i risultati di tali integrali. In questa dimostrazione abbiamo fatto l’ipotesi semplificativa che le corde intercettate siano sempre uniche, in caso contrario gli integrali del secondo e terzo passaggio devono essere separati per considerare i diversi segmenti che compongono la sezione. Ma tale variazione non comporta cambiamenti nella sostanza del ragionamento e quindi nel risultato. Notare che l’implicazione inversa non è vera: due figure con la stessa altezza possono avere la stessa area senza che le corde intercettate dalla stessa retta siano sempre uguali (si pensi, a titolo di esempio, ad un rettangolo di base B e altezza H e un triangolo di uguale altezza e base 2B).
Un ragionamento analogo dimostra la proposizione per il volume. I due integrali che daranno il volume saranno
![]()
Analogamente a prima il fatto che abbiano la stessa altezza ci permette una rototraslazione che rende il dominio di integrazione della variabile z identico per i due integrali mentre, in corrispondenza di ciascuna z, le variabili x e y variano all’interno di una figura la cui forma dipende da z
![]()
Le due parentesi quadre contengono degli integrali di superficie i cui domini di integrazione non sono altro che le sezioni che si ottengono dall’intersezione da un piano orizzontale di quota z rispettivamente con la figura F1 e F2. La situazione descritta può essere visualizzata nella seguente figura in cui sono presenti tre poliedri, di cui uno mistilineo, di uguale altezza ed equivalenti.

Se tali integrali sono uguali, come richiede il Principio di Cavalieri a 3-D, per ogni z allora anche gli integrali in dz saranno uguali e quindi le due figure avranno lo stesso volume. Analogamente a prima abbiamo supposto che le sezioni siano delle figure semplicemente connesse (cioè non composte da figure piane separate senza punti in comume), ma analogamente a prima questa semplificazione non comporta variazioni sostanziali. Come nel caso piano l’implicazione inversa non è vera: due solidi con la stessa altezza possono avere lo stesso volume senza che le aree intercettate dallo stesso piano siano sempre uguali (si pensi, a titolo di esempio, ad un prisma di area di base B e altezza H e una piramide di uguale altezza e base di area 3B).
Come detto prima lo strumento del calcolo integrale non era a disposizione di Cavalieri quando formulò il principio che porta il suo nome per cui il ragionamento che lo convinse della sua plausibilità è certamente diverso. Una possibile ipotesi di dimostrazione intuitiva potrebbe essere la seguente. Eseguiamo il ragionamento direttamente a tre dimensioni perché più significativo e anche perché il Principio di Cavalieri è utile principalmente nella geometria solida.
Il volume di un parallelepipedo in cui tre spigoli ortogonali siano a, b e c è, per definizione, abc. Questa quantità, nel caso in cui le lunghezze siano tutte dei numeri interi in una qualche unità di misura è il numero di cubi di lato 1 (nella stessa unità di misura) che possiamo inserire nel parallelepipedo senza lasciare spazio vuoto. Pertanto possiamo visualizzare il significato della grandezza volume come numero di cubi di lato unitario contenuti nella figura, tale idea, grazie alle proprietà di scomponibilità del volume, può essere estesa anche a figure che non possono essere suddivise in cubi e/o a figure il cui volume non è un numero intero.
Pensiamo ora ad una figura che sia composta da strati di cubi tutti uguali, ciascuno strato poggia su quello sottostante ed eventualmente il numero di cubi varia a piacere da uno strato all’altro (qualcosa di simile a ciò che si può costruire usando i classici giochi di costruzioni a mattoncini). Se io ora, in ciascuno strato, ridispongo i cubi in modo da cambiarne la forma ma senza spostare cubi da uno strato all’altro, otterrò una nuova figura solida ma che con quella di partenza condivide tre cose:
-
il volume, dato che è composta dallo stesso numero di cubi;
-
l’altezza, dato che il numero di strati rimane invariato;
-
l’area di tutte le sezioni orizzontali (cioè l’area di base di ciascuno strato), perché ho ridisposto i cubi all’interno del singolo strato senza cambiare quindi il numero di cubi di ciascun singolo strato.
Naturalmente queste cose sono vere indipendentemente dalle dimensioni dei cubi. Pertanto posso usare cubi molto piccoli e costruire delle approssimazioni di qualunque figura solida che normalmente non è scomponibile in cubi di lato finito. Quanto più i miei cubi saranno piccoli tanto più sarà piccola la differenza tra il solido "vero" e la mia approssimazione "cubettosa". Ma indipendentemente dalla differenza la conclusione vista prima vale per ciascun solido "cubettoso". Posso quindi aspettarmi che le tre proprietà viste prima valgano anche per tutti i solidi.
Come detto prima questa non è una dimostrazione rigorosa perché per poterla portare a termine secondo tutti i canoni richiesti ad una dimostrazione matematica avrei necessariamente bisogno di usare il concetto di limite, non disponibile all’epoca di Cavalieri e che di fatto mi porterebbe alla definizione di Riemann dell’integrale.