Il calcolo richiesto può essere svolto considerando le proprietà matematiche e il senso degli oggetti matematici coinvolti.
Derivare una funzione rispetto ad una variabile significa calcolare, puntualmente o in generale, la rapidità di variazione della funzione al mutare della variabile. Nel caso in esame la funzione è una quantità fisica, il flusso del campo magnetico, mentre la variabile è un’altra quantità fisica, il tempo. A sua volta il flusso si ottiene mediante un’integrale di superficie del campo magnetico.
Dato che nella legge non si fanno restrizioni sul tipo di superficie (se non quelle ovvie, per la natura fisica della legge, che la superficie sia semplicemente connessa, abbia estensione finita e che sia la superficie sia il suo bordo siano quanto meno differenziabili a tratti) allora il flusso risultante dipenderà dal tempo se il campo magnetico varia nel tempo ma anche se il campo magnetico è costante nel tempo ma variabile nello spazio e la superficie si muove (e quindi intercetta zone dello spazio che hanno campi magnetici di differente valore).
Quindi, dal punto di vista strettamente matematico e nel caso più generale possibile, stiamo "semplicemente" considerando la derivata rispetto ad un parametro t di una funzione definita mediante un integrale in cui la funzione integranda dipende dal parametro t oltre che dalle variabili "spaziali" coinvolte nell’integrale e inoltre anche la superficie varia con il parametro t. Quindi vogliamo calcolare l’oggetto dato dall’espressione formale
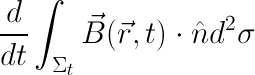
In generale non esiste una formula diretta per calcolare la derivata di un integrale rispetto ad un parametro da cui dipende anche il dominio di integrazione. Ma possiamo aggirare questa difficoltà, con un trucco. Se la superficie di integrazione dipende dal tempo t allora significa che dipendono dal tempo t le equazioni parametriche che la definiscono
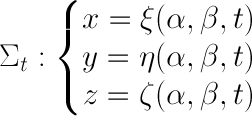 con
con ![]() , parametri della superficie
, parametri della superficie
Se la superficie è regolare queste equazioni sono completamente invertibili, perché, fissato t, deve esserci una corrispondenza biunivoca tra le coppie di valori dei parametri e le terne che individuano tutti i possibili punti della superficie. Pertanto possiamo sfruttare queste equazioni per trasformare l’integrale in un integrale nelle variabili parametriche sul quadrato [0,1]2, e spostare la dipendenza da t della superficie nella funzione integranda mediante le coordinate spaziali.
A questo punto possiamo, grazie alla regolarità delle funzioni coinvolte, invertire l’integrale di flusso con la derivata rispetto a t e quindi derivare direttamente l’integrando senza dover risolvere l’integrale. Tuttavia c’è da notare che molto raramente queta procedura risulta più semplice che risolvere prima l’integrale di superficie e poi calcolarne la derivata.