La gamma di frequenze d’uso di un quadripolo elettrico (filtro, amplificatore ecc.) può essere molto vasta. Per esempio, nello scenario audio la gamma di frequenze va tipicamente da 20 Hz a 20 kHz. In un grafico di unità lineari è quasi impossibile visualizzare in modo chiaro un rapporto di valori 1000:1 (20000/20) e in altri scenari il rapporto della gamma da rappresentare è ancora maggiore.
Così come si utilizza il decibel per la comodità di rappresentare in scala logaritmica una gamma estesa di valori di ampiezza, si rappresentano in unità logaritmiche anche i valori di frequenza o la sua velocità angolare, omega.
In altri termini gli intervalli di frequenza sono espressi in decadi (…0.001, 0.01, 0.1,1,10,100, …Hz) oppure, di norma per reti di segnali audio, in ottave (…1/8,1/4,1/2, 1, 2, 4, 8,16,……Hz).
Qualsiasi rappresentazione di risposta verso un’ampia gamma di frequenze, si utilizzano decadi o ottave per le frequenze. Non c’entra nulla l’ing. H. Bode.
Prima di chiarire “dove si usa" perché e “come si fa” il diagramma di Bode, colgo l’occasione, poiché ritengo utile per tutti coloro che pongono questo tipo di domande, un’introduzione generale sui fondamenti delle risposte dei sistemi elettrici lineari, con componenti a costanti concentrate ed invariabili.
Come ha scritto Pinna, un sistema può essere caratterizzato dalla sua risposta impulsiva. La risposta y (t) d’uscita del sistema è la convoluzione tra l’eccitazione x (t) e la risposta impulsiva h (t), funzione di trasferimento, del sistema.
Un sistema elettrico analogico è un insieme di quadripoli ognuno con una sua funzione elettrica (amplificatore, filtro, attenuatore ecc) al loro interno troviamo una rete di rami e nodi formati da singoli bipoli contenenti uno o più: resistori, R, condensatori, C, Induttori, L, e Generatori, G. Anche i componenti attivi come: valvole termoioniche, transistor, FET, operazionali ecc. sono sempre modellabili come un quadripolo formato da generatori dipendenti ideali più le inevitabili R, C, L intrinseche.
Ebbene per ottenere l’effetto voluto all’uscita del sistema y (t) fissato il segnale d’ingresso, causa, x (t) e data una configurazione elettrica, significa calcolare gli elementi della rete mediante equazioni differenziali alle derivate parziali.
Un conto è analizzare nel dominio del tempo pochi elementi R, C, L un altro analizzare un sistema molto complesso. Impossibile anche per un esperto matematico. Basti pensare che questo percorso non fu mai praticato neanche negli anni sessanta quando fu disponibile l’accesso, tramite schede perforate, ai grossi centri di calcolo.
Anche ricavare sperimentalmente la risposta y ( t) non si ottengono ottimi risultati. L’impulso di Dirac è impossibile da realizzare fisicamente. Per scopi pratici, si possono produrre impulsi che si avvicinano al Dirac. Spesso è più semplice usare una eccitazione impulsiva detta “ a gradino “. Un gradino ideale non è realizzabile perché il tempo di salita dovrebbe essere nullo e la durata infinita. Tra l’altro, minore è il tempo di salita maggiore è il costo di un oscilloscopio che diventa improponibile per molte università o piccole aziende elettroniche.
In pratica si è sempre progettato reti lineari nel dominio della frequenza poiché è molto più semplice sia calcolare la risposta in frequenza H (f) con più familiari equazioni algebriche che ottenerla sperimentalmente con generatori sinusoidali.
La risposta in uscita è ancora una sinusoide avente la medesima frequenza di quella d’ingresso ma di ampiezza e fase diverse.
Anche la verifica sperimentale è semplice basta eccitare il sistema tramite segnali sinusoidali e misurare l’ampiezza e la fase dell’uscita in rapporto a quelle d’ingresso.
E’ possibile dimostrare che l’ampiezza e fase della sinusoide in uscita si ottiene moltiplicando l’ampiezza della sinusoide d’ingresso per la funzione di trasferimento H (s) dove s=jω, iota omega, è una variabile complessa.
La H (s) ha il significato fisico di trasformata di Laplace della risposta impulsiva a delta di Dirac. Sarà sempre possibile, se interessa, in qualsiasi momento, passare da una risposta in frequenza H (s) alla risposta all’impulso h (t) mediante l’antitrasformata di Laplace e viceversa (Chi vorrà approfondire capirà meglio il significato di "s").
Con la conoscenza della teoria delle reti, in pratica l’uso dei principi di Kirchhoff in forma complessa considerando le impedenze sui rami e nodi della rete formate dagli elementi R, C e L come insieme di reattanze in regime sinusoidale R, jωL, 1/jωC, si ricava in forma complessa la funzione H (s) della rete.
Dove il modulo, lH (s)l, rappresenta la risposta ampiezza verso frequenza e l’argomento di H (s) la risposta fase verso frequenza.
Le funzioni che si ricavano sono del tipo razionali fratte. Sono uguali al rapporto tra due polinomi. Il numeratore ha sempre la forma: a+a1 s+… + a m S m ed il denominatore b+b1 s+ -. + a n S n .
Si dice grado o ordine della rete il più alto esponente della variabile s.
Un sistema stabile avrà sempre il grado del numeratore minore del grado del denominatore quindi, dall’analisi matematica, facendo tendere la frequenza a infinito la H (s) tenderà zero. Dal quadripolo non uscirà nulla, come realmente avviene fisicamente nella realtà.
I coefficienti a e b sono sempre reali, grandezze fisiche R, C, L costanti, K, altrimenti la rete non sarebbe realizzabile. Le radici del polinomio al numeratore, gli ”zeri “, per quanto detto, sono reali o a coppie complesse coniugate e cosi i “poli”, che ricordiamo sono le radici dei polinomi al denominatore ( In soldoni, la ricerca delle intersezioni con l’asse delle ampiezze ( y ) quando i valori di s rendono il numeratore = 0 ( zeri ) e l’intersezione con l’asse x, delle frequenze o pulsazioni omega, quando i valori di s rendono il denominatore = 0 ( poli ).
Maggiore è l’ordine del quadripolo maggiore è la pendenza della variazione di ampiezza verso frequenza. La rete si comporta come un filtro. Secondo della posizione dei poli o zeri sull’asse cartesiano. Il filtri possono essere: passa-basso, passa-alto, passa banda o stoppa banda.
Calcolando la funzione polinomiale verso punti di frequenza noi otteniamo un grafico preciso della funzione di trasferimento. Ma, il calcolo per funzioni oltre il terzo grado è spesso laborioso. Oggi, nell’era del computer tutto ciò farà sorridere, ma l’ing Bode che si occupava negli anni trenta di sistemi di controllo e telecomunicazioni lo sapeva benissimo ed escogitò un pratico sistema in modo da velocizzare i calcoli.
Ecco, i diagrammi di Bode sono un modo approssimativo per ottenere velocemente la funzione di trasferimento in modulo e fase della H (s) .
Schizzando pochi ma, rapidi essenziali segmenti rettilinei si ottengono le stesse informazioni degli esatti curvilinei diagrammi di ampiezza e fase calcolato per punti di frequenza.
Tralasciando alcune importanti regole dei numeri complessi sulla manipolazione della funzione di trasferimento vediamo come si procede, solo per l’ampiezza verso frequenza, con esempio di una semplicissima rete che rappresenta un amplificatore audio da 20 Hz a 20 kHz.
Dallo schema elettrico si individuano le più semplici sottoreti possibili.
In figura osserviamo all’ingresso una rete passa – alto formata da R1 e C1 (Le frequenze prossime a zero non sono trasmesse da C1 che non lascia passare la componente continua).
Segue un amplificatore contro-reazionato negativamente che non ha elementi reattivi quindi la funzione di trasferimento verso frequenza è una costante.
La rete termina con un filtro Passa-Basso poiché alle frequenze alte C2 tende a diventare un corto circuito. La funzione lH (s)l tende a zero a frequenze infinite.
Ora grazie alla teoria delle reti, calcoliamo le semplici funzioni di trasferimento delle tre sottoreti H1 (s), H2 (s) e H3 (s).
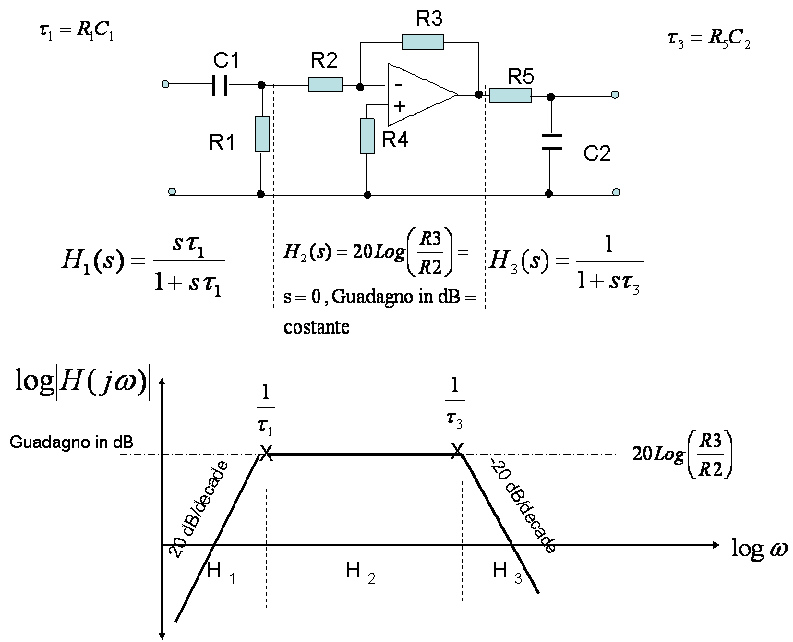
Disegniamo una rappresentazione cartesiana. E’ più comodo collocare sull’ascissa,X, i valori della pulsazione ω in unità logaritmica (Basta dividere per 6,28 e otteniamo i valori di frequenza). Sull’asse delle ordinate,Y, si rappresentano i valori d’ampiezza del modulo di H (s) in dB. L’asse positivo di Y rappresenta il guadagno della rete. L’asse negativo di Y rappresenta l’attenuazione della rete. I valori rappresentati vanno da + infiniti dB a – infiniti dB. Ciò è molto importante perché in presenza di zeri non vedremo mai la funzione attraversare il valore zero di y, come si è abituati a tracciare il grafico di funzioni in matematica, ma tenderà verso – infiniti dB (discorso simile per i poli).
Individuiamo subito le funzioni indipendenti dalla frequenza, s=0. Inseriamo nell’equazione i valori dei componenti e calcoliamo il valore di H2.
In questo caso è un guadagno e tracciamo una retta paralella all’asse delle frequenze in corrispondenza al valore in dB dell’asse Y.
Si localizza la rete dipendente dalla più alta frequenza. Nel nostro caso H3 (s) e la si analizza. Osserviamo che H3 (s) non potrà mai avere un valore di s tale da portare il numeratore a zero. La rete ha un solo polo corrispondente a -1/Tau3 .
Si posiziona il polo alla frequenza calcolata, come in figura.
Poiché la funzione H3 (s) è del primo ordine la semiretta da tracciare dal valore del polo ha una pendenza verso frequenze infinite di 20 dB per decade o 6 dB per ottava di frequenza.
Fosse stata del 2°, 3° o 4 ° avremmo avuto rispettivamente una pendenza di 12,18,24 dB per ottava oppure 40,60,80 dB per decade.
Ora rimane da analizzare la funzione della rete H1 (s), vediamo che il numeratore si annulla per s=0 e quindi abbiamo uno zero sull’origine. Il denominatore si annulla per 1/Tau1 . Calcoliamo il valore e posizioniamo il polo come abbiamo fatto per la funzione H3 (s).
Fine. Con tre colpi di matita conosciamo la risposta in ampiezza frequenza della rete. Più facile a farsi che spiegarlo.
Bode dimostrò che se la rete è stabile è sufficiente la conoscenza del diagramma d’ampiezza per risalire al diagramma di fase, ma questo è un altro discorso ….
Gianfranco Verbana