Se per valutare si intende ricavare un’espressione analitica per le tre componenti del campo magnetico valida per tutti i punti che non giacciono sull’asse centrale, allora la risposta è negativa, perchè tale calcolo analitico, per poter essere portato a termine esattamente, necessita di risolvere degli integrali ellittici, per i quali non esiste, almeno finora, una soluzione analitica.
Se invece ci si accontenta di risolvere approssimativamente tali integrali e di dare una rappresentazione grafica del campo mediante linee di forza, allora è possibile rispondere affermativamente. L’analisi è per certi versi simile a quella che si svolge per il campo sull’asse della spira, si analizzano le simmetrie della distribuzione di corrente e questo porta a concludere che il campo magnetico giace sempre sul piano che passa per l’asse della spira e il punto in cui si calcola il campo. L’unica differenza è che lontano dall’asse il campo possiede sia una componente perpendicolare alla spira sia una componente perpendicolare all’asse (nel caso del calcolo del campo sull’asse invece tale componente è sempre nulla).
Il sistema possiede una simmetria cilindrica per cui l’andamento delle linee di forza è uguale per tutti i piani che passano per l’asse della spira. Rappresentando queste linee di forza si ottiene la seguente figura qualitativa
.jpg)
L’asse z corrisponde all’asse della spira, mentre la coordinata r misura sostanzialmente la distanza da tale asse, anche se nel disegno, con un abuso grafico, abbiamo considerato anche valori negativi di r per poter disegnare la situazione completa per un dato piano. Il cerchio rosso con un pallino al centro è il punto in cui la corrente attraversa il piano con verso uscente, il cerchio rosso con la croce è invece il punto in cui la corrente entra nel piano.
È possibile dare un’espressione analitica per le due componenti del campo magnetico in alcuni casi limite.
Per piccoli valori di z e r
![]() ,
, 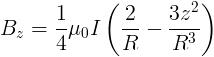
Per piccoli valori di z e grandi valori di r
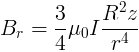 ,
, 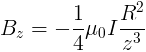
Infine per grandi valori di z
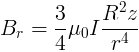 ,
, 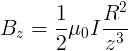
Le componenti per piccoli valori di r e grandi valori di z sono quelle che si ottengono considerando il campo sull’asse.