Per ottenere il risultato richiesto è più comodo calcolare innanzitutto la probabilità che n numeri estratti a caso nell’intervallo compreso tra 0 e 1 abbiano somma inferiore a 1. Se estraggo a caso un numero x1 compreso tra 0 e 1 la probabilità p1 che questo numero sia inferiore a 1 è ovviamente 1.
Una volta estratto il primo numero la probabilità che la sua somma con un secondo numero x2 sia ancora inferiore a 1 è 1−x1, perché il secondo numero, per non superare 1 come somma, deve appartenere ad un intervallo più ristretto rispetto a quello dei numeri compresi tra 0 e 1. Per conoscere la probabilità generale p2 che due numeri abbiano somma inferiore a 1 dobbiamo integrare su tutti i possibili valori di x1, quindi
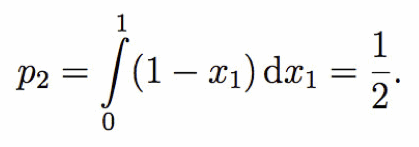
Analogamente, una volta estratti due numeri compresi tra 0 e 1, la probabilità che la somma con un terzo numero x3 sia inferiore a 1 è 1−x1−x2. Quindi
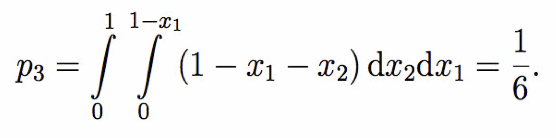
L’estremo superiore dell’integrale più interno è 1−x1 perché il numero x2 deve essere scelto in un sottoinsieme più ristretto dell’intervallo compreso tra 0 e 1 per poter soddisfare la condizione che la somma sia inferiore a 1.
In generale quindi possiamo scrivere che la probabilità pn che n numeri scelti a caso nell’intervallo compreso tra 0 e 1 abbiano somma inferiore a 1 è data da
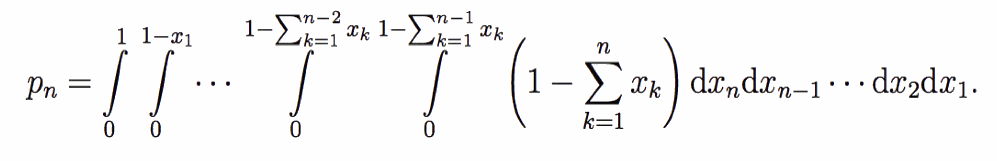
Operiamo il cambio di variabile multiplo
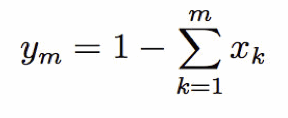
il cui jacobiano è unitario, quindi
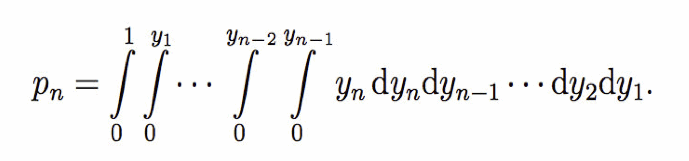
Dato che, in generale, la primitiva di yh è yh+1/(h+1), i diversi integrali da eseguire in successione hanno l’unico effetto di aggiungere un fattore intero, ad ogni integrale aumentato di 1, al denominatore. Per cui evidentemente il risultato finale sarà
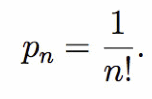
La probabilità Pn che la somma degli n numeri superi 1 è naturalmente la probabilità complementare a questa,
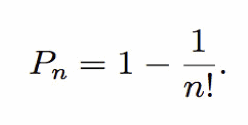
Per calcolare la media richiesta nella domanda occorre innazitutto calcolare la probabilità che si superi 1 esattamente con n-mo addendo. Questa probabilità è la probabilità che all’n-mo addendo si sia superato 1 meno la probabilità che questo sia avvenuto con l’addendo precedente
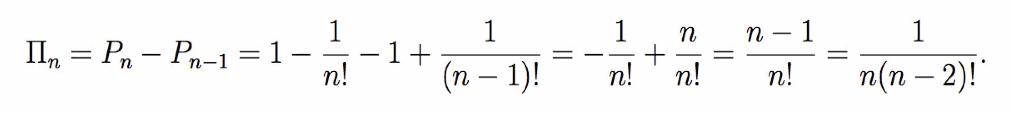
Il numero medio di addendi per superare 1 è dato quindi dalla serie
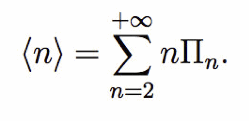
La serie parte da n=2 perché naturalmente è impossibile avere una somma superiore a 1 con un solo addendo minore o uguale di 1, per cui gli addendi relativi a n<2 sono nulli. Procedendo con il calcolo evidentemente
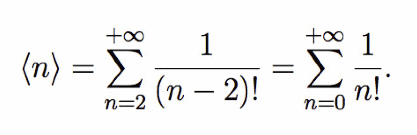
Tenendo presente che
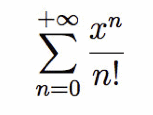
è la serie che definisce la funzione esponenziale di base naturale ex, allora la serie che fornisce il numero medio di n è il valore che questa funzione assume per x=1, cioè il valore e.
Si ringrazia sentitamente Daniele Malesani per l’indispensabile aiuto fornito nell’editare questa risposta.