Il grafico della funzione y=ax2+bx+c, con x ∈ R e a ≠ 0, è rappresentato da una generica parabola con asse di simmetria parallelo all’asse y. In particolare tale parabola ha:
– asse di simmetria di equazione x=-b/2a
– vertice nel punto V=(-b/2a,-∆/4a)
– fuoco nel punto F=(-b/2a,(1-∆)/4a)
essendo ∆=b2-4ac. Analizziamo singolarmente il variare di a,b,c, tenendo man mano fermi due parametri e solo uno variabile.
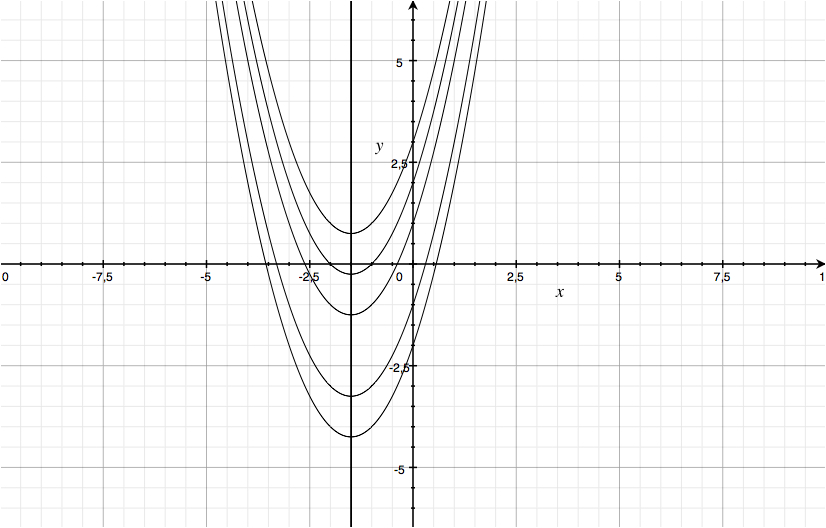
1) Il caso più facile è rappresentato dal caso c variabile, a e b fissati. Infatti in tal caso otteniamo una famiglia di parabole con lo stesso asse di simmetria, con vertice variabile sull’asse di simmetria e con fuoco pure variabile sullo stesso asse.
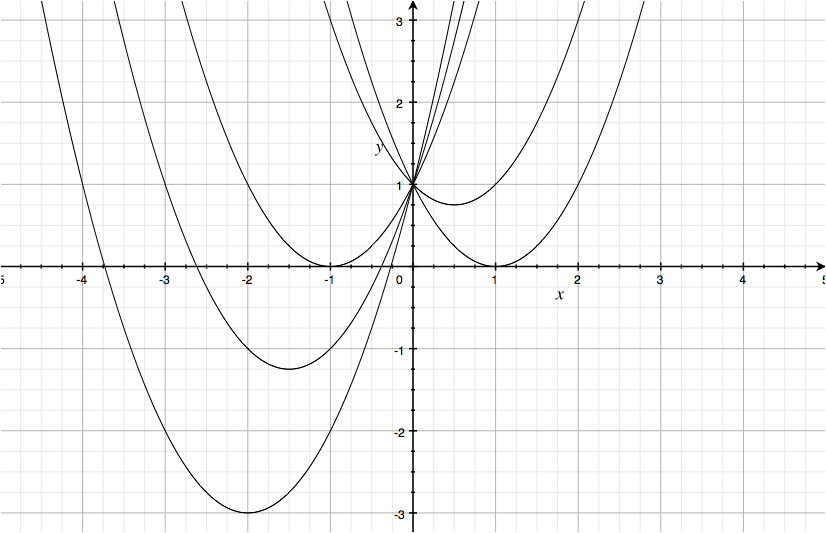
2) Trattiamo il caso in cui sia b variabile e i parametri a,c siano fissati. In tal caso la famiglia di parabole di equazioni y=ax2+bx+c rappresenta una famiglia di parabole che passano tutte per uno stesso punto appartenente all’asse y. Infatti consideriamo due parabole distinte di equazioni rispettive y=ax2+b1x+c e y=ax2+b2x+c; allora il punto di interesezione tra esse si ottiene mettendo in sistema le due equazioni date, sistema che porta a ax2+b1x+c=ax2+b2x+c, ovvero x=0, dal momento che b1 ≠ b2. Dunque il punto di intersezione tra le due parabole date ha coordinate (0,c); ma tale punto appartiene ad ogni parabola di equazione y=ax2+bx+c con a,c fissati e b variabile, e quindi tutte le parabole così fatte passano per il punto (0,c). Tali parabole inoltre hanno tutte la stessa "apertura", come la seguente figura illustra.
3) Infine trattiamo il caso in cui sia a variabile, con b e c fissati. Per avere l’equazione di una parabola, come detto all’inizio, deve essere necessariamente a ≠ 0; nel caso in cui si abbia a=0 l’equazione diventa y=bx+c la quale rappresenta una generica retta nel piano, non verticale. Nel caso in cui a possa dunque variare in R – {0} si ottiene una famiglia di parabole che passano tutte per il punto (0,c) (dimostrazione analoga al caso 2), che possono anche cambiare concavità e che diventano sempre più ripide man mano che |a| cresce; in tal caso, a differenza del punto precedente, le parabole quindi diminuiscono la loro apertura se |a| assume valori grandi.
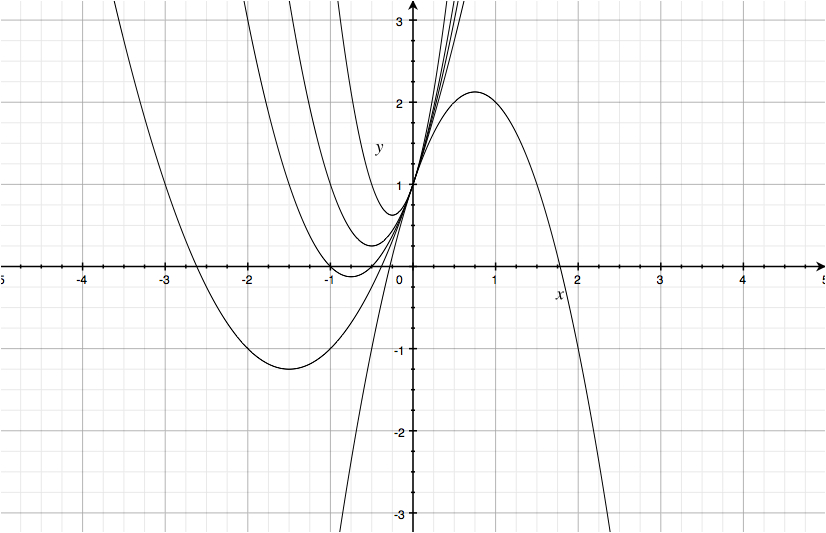
Quando a → +∞ osserviamo che l’asse di simmetria tende ad avere equazione x=0, ovvero tende a essere l’asse y; inoltre il vertice che ha coordinate (-b/2a,-∆/4a) tende al punto di coordinate (0,c), dal momento che
lima → +∞-∆/4a=lima → +∞(4ac-b2)/4a=c.
L’apertura della parabola infine diviene sempre più sottile, per cui per a → +∞ la parabola di equazione y=ax2+bx+c, con b,c fissati, tende a coincidere con la semiretta (c,+∞) giacente sull’asse y. Un discorso analogo si può fare nel caso a → -∞.