Quando nelle microstrip è presente dielettrico con costante complessa, come si trova la costante di propagazione e la costante dielettrica effettiva?

Quando si considerano le perdite di un dielettrico, la permeabilità, permettività o costante (tre modi diversi per dire la stessa cosa) dielettrica è sempre rappresentata in forma complessa.

Esistono solo materiali con perdite o considerati senza perdite, ideali, quando per semplificare i calcoli ci viene comodo di trascurare le perdite.

Tutti i materiali (a parte il vuoto) come vedremo, hanno una permeabilità complessa.

Il problema è che nei testi scolastici e non, si ignora spesso che la diffusione: dalla costante dielettrica, alla costante di propagazione, sono tutte classiche formule ricavate dalle equazioni di Maxwell, considerando i mezzi trasmissivi senza perdite.

Per fortuna che l’unica modifica delle equazioni di Maxwell da introdurre, se si considera il mezzo trasmissivo con perdite, riguarda solo l’equazione d’Ampère. In questo caso possiamo usare la forma fasoriale¹ della legge di Ampère (per onde piane sinusoidali e mezzo trasmissivo: omogeneo, isotropo e lineare) ed introdurre la perdita come conduttanza elettrica, σ.

Osserviamo che ora vi sono due componenti di correnti nella legge di Ampère: una densità di corrente di conduzione (σ x E) a cui è associata una perdita di potenza e l’altra una densità di corrente di spostamento (jωε x E)ε con una permettività complessa, episilon con cappello: a cui è associato un immagazzinamento di potenza. Confrontando le due espressioni (con e senza perdite ) si può vedere che si può modificare il risultato per il caso senza perdite in modo che venga incluso la situazione reale con perdita sostituendo il noto epsilon,

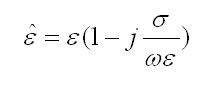
Il termine:

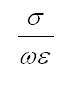
è chiamato tangente di perdita del materiale ed è funzione della frequenza. I valori della tangente di perdita vengono misurati sperimentalmente per vari materiali e si trovano tabulati sui libri specialistici per parecchie gamme di frequenza.

Come vedete una grande e bella differenza dalle classiche tabelle di sola permettività per i dielettrici o di conduttività per i conduttori.

In conclusione è il rapporto tra queste due potenze o correnti (conduzione e spostamento) l’indice dell’entità delle perdite del mezzo trasmissivo. Con la conoscenza della tangente di perdita abbiamo un ben preciso criterio di valutazione di corpi conduttori e isolanti in funzione della frequenza (e non alta o bassa conduttività o alto a bassa permeabilità, senza considerare la frequenza d’impiego).

Scrissi in una mia precedente risposta:
http://www.vialattea.net/esperti/php/risposta.php?num=10714

“Un materiale conduttore a bassa frequenza, può diventare isolante in alta frequenza. Un materiale è un buon conduttore quando il rapporto tra la conduttanza specifica, σ, e il prodotto tra frequenza e costante dielettrica, ε , è >>1 (buon dielettrico se è <<1) “.

I materiali sono quindi classificati a secondo che la corrente di conduzione sia maggiore o minore rispetto alla corrente di spostamento ad un determinato valore di frequenza.

Invece, la costante di propagazione, Υ, chiamata effettiva nella domanda, che tiene conto delle perdite, e quindi della costante complessa del dielettrico del microstrip è uguale a:

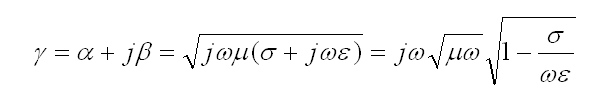
Se il dielettrico del microstrip alla frequenza di utilizzo è particolarmente buono tale che la tangente di perdita risulti:

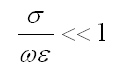
L’espressione della costante di propagazione si semplifica notevolmente e diventa la forma classica dello spazio libero:

Oltre alla perdita di tipo conduttivo che ho descritto, i dielettrici possiedono anche altri meccanismi di perdita. Essi sono caratterizzati da microscopici dipoli formati dalle cariche. Al crescere della frequenza del campo questi dipoli non possono allinearsi completamente con il campo elettrico ma si orientano solo parzialmente. Anche per questa perdita si tiene conto attribuendo una permettività complessa del materiale. Questo fenomeno è descritto da Dario Benvenuti. http://www.vialattea.net/esperti/php/risposta.php?num=13329

Note:

1. Dando per scontato la conoscenza delle due importanti operazioni del calcolo vettoriale, la divergenza ed il rotore applicate al teorema di Stokes per le equazioni di Maxwell, un’altra notevole semplificazione di rappresentazione e di calcoli è quella di sostituire i vettori di campo con i fasori. Condizione necessaria è che i vettori di campo, che in generale possono avere una dipendenza casuale nel tempo, devono avere un andamento sinusoidale verso l’asse dei tempi per un tempo lungo tale da eliminare eventuali transitori iniziali, si suol dire che il campo deve essere in “regime sinusoidale permanente“. Ovviamente, come scrive Lussardi tutti i vettori devono pure avere la stessa frequenza, omega.

Per esempio l’espressione fasoriale della componente lungo l’asse x del vettore di intensità di campo magnetica H_x è:

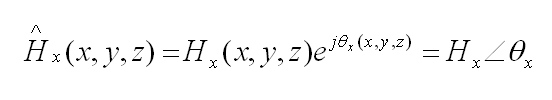
I fasori sono quantità complesse e la loro espressione nel dominio del tempo si ottiene moltiplicandoli per e^jωt e considerando la parte reale del risultato.

Per risolvere, in questo contesto, le equazioni di Maxwell si sostituiscono i vettori di campo con i corrispondenti fasori moltiplicati per e^jωt. Derivando i fasori rispetto al tempo si ottiene:

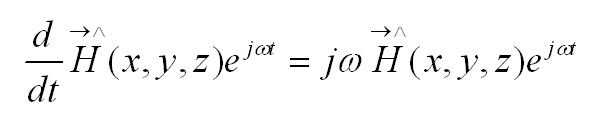
E una importantissima proprietà che permette anche a coloro che hanno conoscenza della matematica di media superiore la risoluzione delle equazioni di Maxwell (leggi parte finale risposta di Lussardi). La forma fasoriale delle equazioni di Maxwell si ottiene quindi sostituendo i vettori di campo con i corrispondenti fasori semplificando, poiché è sottointeso, il termine comune esponenziale in modo che il tempo non compaia da nessuna parte.

Come esempio la legge di Amperè dell’equazione di Maxwell in forma fasoriale diventa:

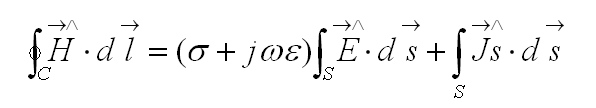
Ricordando il teoerema di Stokes otteniamo sempre in forma fasoriale:

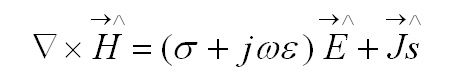
Tutto ciò, ripeto, è valido per onde piane sinusoidali e mezzi trasmissivi lineari, omogenei ed isotropi.

Gianfranco Verbana