Innanzitutto ricordiamo la definizioni dei diversi sistemi di coordinate.
Una volta fissato un sistema di riferimento ortogonale 3D nello spazio le coordinate cartesiane del punto P si ottengono semplicemente dalle proiezioni ortogonali su ciascun asse:
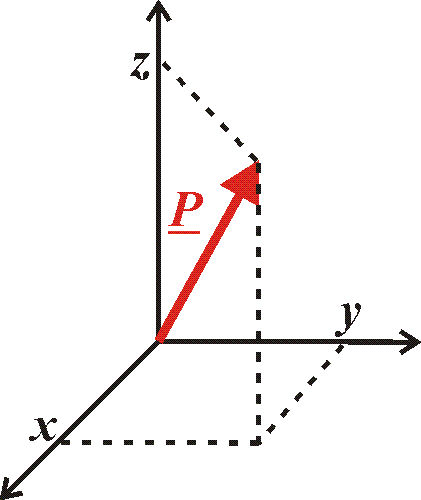
Le coordinate cilindriche conservano la coordinata z di quelle cartesiane ma sostituiscono le altre due con la coordinata r, che è la distanza tra la proiezione del punto P sul piano xy e l’origine, e la coordinata angolare θ, che è l’angolo formato tra il segmento che individua r e l’asse x:
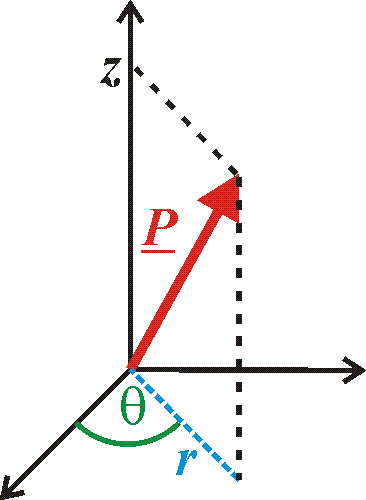
Dalla definizione si ricavano facilmente le formule di passaggio con le coordinate cartesiane:
x=r cosθ, y=r sinθ
e
r=√(x2+y2), θ=arctan(y/x) [+π se x è negativo].
Le coordinate sferiche abbandonano completamente quelle cartesiane, a fianco della coordinata angolare θ, identica a quella cilindrica, viene introdotta un’altra coordinata angolare φ, che è l’angolo formato tra il vettore posizione di P e l’asse z, inoltre compare ancora una coordinata indicata con r, ma stavolta è la distanza completa tra P e l’origine degli assi:
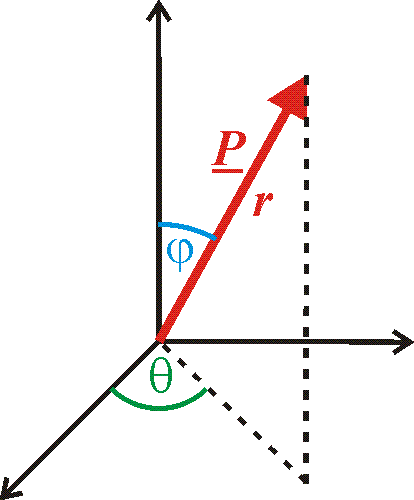
Anche in questo caso è facile calcolare le formule di passaggio alle coordinate cartesiane:
x=r sinφ cosθ, y=r sinφ sinθ, z=r cosφ
e
r=√(x2+y2+z2), θ=arctan(y/x) [+π se x è negativo], φ=arccos[z/√(x2+y2+z2)].
Per poter eseguire le derivate rispetto al tempo del vettore posizione P è comodo considerarlo scomposto in maniera opportuna a seconda del insieme di coordinate che si utilizza. Nel caso delle coordinate cartesiane è comodo considerare il vettore P scritto così
P=x Ex+y Ey+z Ez
dove Ex, Ey ed Ez sono i versori degli assi (cioè vettori di modulo 1 orientati esattamente come gli assi cui si riferiscono), le cui componenti sono Ex=(1,0,0), Ey=(0,1,0) ed Ez=(0,0,1). Le derivate per ottenere velocità V e accelerazione A sono facili da eseguire, in quanto i tre versori sono costanti nel tempo
V=P‘=x’ Ex+y’ Ey+z’ Ez
A=P”=x” Ex+y” Ey+z” Ez
da cui ricaviamo immediatamente che la velocità è un vettore le cui componenti cartesiane sono le derivate prime delle componenti cartesiane del vettore posizione rispetto al tempo e l’accelerazione è un vettore le cui componenti cartesiane sono le derivate seconde delle componenti cartesiane del vettore posizione rispetto al tempo.
Nel caso delle coordinate cilindriche è comodo esprimere il vettore P nel modo seguente:
P=r Θθ+z Ez
dove Θθ è il versore della proiezione di P sul piano xy, con componenti Θθ=(cosθ,sinθ,0). Procedendo alla derivata prima osserviamo che dei due versori solo Ez è costante nel tempo, per cui la derivata del primo dei due addendi dovrà essere eseguita con la formula della derivata di un prodotto [(f g)‘=f‘ g+f g‘], per cui si ha
V=P‘=r’ Θθ+r Θθ‘+z’ Ez
ma Θθ‘=θ‘ (-sinθ,cosθ,0)=θ‘ Θθ+π/2, quindi
V=P‘=r’ Θθ+r θ‘ Θθ+π/2+z’ Ez
da cui si deduce che se l’unico movimento del vettore P è una rotazione intorno all’asse z allora la velocità sarà perpendicolare a P (in quanto l’unico termine non nullo di questa derivata sarebbe quello relativo al versore Θθ+π/2) che è ruotato di π/2 rispetto a Θθ. Passando alla derivata seconda, per avere l’accelerazione, otteniamo
A=P”=r” Θθ+2 r’ θ‘ Θθ+π/2+r (θ” Θθ+π/2+θ‘ Θθ+π/2‘)+z” Ez
analogamente a prima Θθ+π/2‘=θ‘ Θθ+π=–Θθ, per cui
A=P”=r” Θθ+2 r’ θ‘ Θθ+π/2+r (θ” Θθ+π/2–θ‘2 Θθ)+z” Ez.
Analogamente a prima, nel caso di sola rotazione intorno all’asse z l’accelerazione risulterà essere un vettore diretto istante per istante verso l’asse di rotazione.
Nel caso delle coordinate sferiche è opportuno rappresentare P nella forma
P=r Ωθ,φ
dove Ωθ,φ è il versore di P e quindi Ωθ,φ=(sinφ cosθ,sinφ sinθ,cosφ). Procedendo alla derivata prima
V=P‘=r’ Ωθ,φ+r Ωθ,φ‘
ma
Ωθ,φ‘=(–θ‘ sinφ sinθ+φ‘ cosφ cosθ,θ‘ sinφ cosθ+φ‘ cosφ sinθ,–φ‘ sinφ)=
=θ‘ sinφ (–sinθ,cosθ,0)+φ‘ (cosφ cosθ,cosφ sinθ,–sinφ)=
=θ‘ sinφ Θθ+π/2+φ‘ Ωθ,φ+π/2,
quindi
V=P‘=r’ Ωθ,φ+r (θ‘ sinφ Θθ+π/2+φ‘ Ωθ,φ+π/2).
Procedendo alla derivata successiva si ottiene l’accelerazione,
A=P”=r” Ωθ,φ+2 r’ (θ‘ sinφ Θθ+π/2+φ‘ Ωθ,φ+π/2)+
+r [sinφ (θ” Θθ+π/2–θ‘2 Θθ)–φ‘2 Ωθ,φ+φ” Ωθ,φ+π/2]
per ottenere questo il risultato è stato tenuto conto di quanto calcolato prima per Ωθ,φ‘ e che Θθ+π=–Θθ, Ωθ,φ+π=–Ωθ,φ.