È purtroppo un errore comune in molte opere di divulgazione ma anche (purtroppo) in molti testi per le superiori, quello che evidentemente ispira la domanda. L’errore consiste, in pratica, nel mettere il principio di indeterminazione praticamente ovunque, anche laddove non si deve. Il principio di indeterminazione è in effetti un teorema della Meccanica Quantistica, che correla l’incertezza nella misura di “coppie” di quantità fisiche (tecnicamente: coppie di quantità canonicamente coniugate), nella forma:
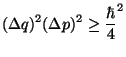 ” />
” />
Questo “principio”, però, è solo un “principio negativo”, non può essere usato da solo in maniera “costruttiva”, per determinare per esempio l’evoluzione delle quantità fisiche. Asserisce che su uno stato (per esempio) se determino con molta precisione la posizione, perdo molta precisione sulla misura dell’impulso1. Questo non vuol dire che l’impulso aumenta: infatti non posso dire nemmeno se aumenta o diminuisce, essendo ancora meno determinato di prima della misura della posizione.
Spieghiamo meglio invece il problema: abbiamo una particella (la carica in questo momento non ha importanza) che è vincolata da un potenziale a stare entro il volume di "una scatola". Assumiamo che le collisioni con le pareti siano elastiche (in genere dipende dal potenziale scelto). All’interno di questa scatola però non è soggetta ad alcuna forza. Classicamente, allora, la particella non farebbe altro che rimbalzare tra le pareti, e, come è noto, mantenere energia costante. È possibile anche calcolare quale sarà la forza mediata sul tempo sentita dalle pareti per effetto degli urti, che e’ proporzionale alla pressione. Fin qui è tutto noto. Ed è noto anche che avvicinando due pareti la forza media sentita dalle pareti stesse nell’unità di tempo aumenti. Infatti aumenta la frequenza degli urti con le pareti stesse, per cui nell’unità di tempo la particella trasmetterà un impulso maggiore alle pareti.
Affrontiamo il problema quantisticamente. Non è possibile in questa sede entrare nei dettagli, per cui sarò molto sintetico (e purtroppo approssimativo). Supponiamo adesso che la scatola abbia i vertici, in un sistema ortogonale di coordinate, nei punti
La meccanica quantistica ci permette di calcolare quali siano i livelli energetici della particella, cioè quali siano i possibili valori che risultano da una misura della energia del sistema. Il risultato è
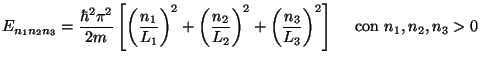 ” />
” />
laddove m è la massa della particella, e
![]() ” /> sono numeri interi positivi.
” /> sono numeri interi positivi.
Come si vede, i livelli energetici dipendono dalle distanze tra le pareti. In tutto ciò il principio di indeterminazione però non ha avuto alcun ruolo. Non sarebbe stato possibile calcolare i livelli energetici in base alle incertezze sull misure.
Ma come va interpretato questo aumento di energia? In realtà è molto semplice, e si capisce anche soltanto in maniera classica2. Per avvicinare le pareti, bisogna agire contro la forza che la particella esercita su di esse. Pertanto, bisogna produrre un lavoro, che è equivalente a dire che bisogna fornire energia al sistema.
Note:
- … dell’impulso1
- momentum è il termine latino introdotto da I.Newton nei suoi Principia, e in inglese viene usato anche in forma colloquiale, come in “The enterprise gained more and more momentum” (“L’impresa ha guadagnato sempre più slancio”). In italiano si preferisce usare il termine impulso, oppure momento, per quanto quest’ultimo prevalentemente nelle locuzioni “momento angolare”, o “momento di una forza rispetto a un asse”.
- … classica2
- Di passata, notiamo anche che essendo il sistema delle pareti macroscopico, alla scatola in quanto sistema fisico si può applicare tranquillamente la meccanica classica.