Vorrei fare giusto una breve introduzione per fare un po’ di chiarezza. La letteratura fantascientifica abbonda di storie in cui qualcuno si trova (magari intrappolato suo malgrado) in "un’altra dimensione", nella quale le cose succedono in maniera diversa. Il senso in cui viene inteso in questi racconti il termine "dimensione" è quello colloquiale, e pertanto piuttosto impreciso. Nella migliore letteratura fantascientifica, invece, viene in genere usato il termine "universo parallelo", o simili derivati. Splendido esempio, oltreché canonico dal punto di vista della letteratura fantascientifica, è "Neanche gli dei…" di I.Asimov, in cui (non svelero’ i dettagli della storia per ovvi motivi) si narra di universi paralleli in cui le interazioni nucleari hanno intensità diverse [1].
Inoltre, anche nella letteratura scientifica si trovano scenari in cui ci sono più universi, più o meno interagenti tra di loro. Il campo a cui appartengono queste ricerche è quello della Cosmologia. Percio’ non è né impensabile né assurda l’idea di avere più "universi paralleli", anche se ovviamente qualunque teoria scientifica deve passare i test canonici di validità, e per quanto riguarda la Cosmologia le teorie non sono (allo stato attuale) molto avanti, confrontate con gli altri campi della Fisica.
Veniamo all’argomento della domanda, partendo da questa questione: è possibile che in certe condizioni "il tempo", cioè "quello che viene misurato dall’orologio" scorra in maniera diversa?
Come ormai arcinoto grazie alla divulgazione scientifica, è vero che si possono creare condizioni per cui il tempo per un osservatore scorra a velocità diversa rispetto a quello di un altro osservatore. Prima di andare oltre, preciso che quando si dice "il tempo secondo un osservatore" si intende il tempo segnato da un orologio portato dall’osservatore in questione. Il termine preciso per indicare il tempo secondo l’orologio portato da un osservatore è “tempo proprio” di quell’osservatore. L’orologio in sé è nient’altro che un sistema che compie una sequenza periodica di trasformazioni, e il tempo che impiega a completare un intero periodo è conoscibile grazie alle Leggi della Fisica. Per cui se portiamo un orologio in un luogo o in una condizione in cui il tempo “scorra diversamente” (vedremo meglio in che senso nel seguito), questo continuerà a compiere le sue trasformazioni, definendo la misura del tempo per l’osservatore che “porta quell’orologio”, ed è secondo questa misura che sperimentiamo gli effetti del tipo “dilatazione temporale”.
Un esempio standard è quello del cosiddetto "Paradosso dei due gemelli": in effetti non è per niente un paradosso nel senso della logica, solo un effetto relativistico che va contro quello che potremmo chiamare "l’abituale modo di pensare". L’effetto su cui si basa questo fenomeno è quello noto col nome di "dilatazione temporale". Secondo la Relatività, l’intervallo unitario di tempo segnato da un orologio che si muove ad una certa velocità v rispetto ad un laboratorio "inerziale" (cioè solidale con un sistema di riferimento inerziale) risulta dilatato rispetto all’intervallo di tempo unitario segnato da un orologio solidale col sistema del laboratorio; il fattore di dilatazione è
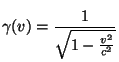 ” />
” />
laddove ![]() ” /> è la velocità della luce nel vuoto,
” /> è la velocità della luce nel vuoto,
![]() ” />. Per maggiori dettagli vedere [2].
” />. Per maggiori dettagli vedere [2].
Un esercizio elementare classico per gli studenti di Fisica del primo anno, è quello di spiegare come è possibile che si possano rilevare dalla superficie della Terra i muoni dei raggi cosmici secondari, che vengono prodotti quando per es. i protoni dei raggi cosmici primari collidono con le molecole dell’alta atmosfera terrestre. Il nocciolo del problema è che tali muoni decadono nel tempo di 2.2 microsecondi. Anche se avessero la velocità della luce, non riuscirebbero a percorrere più di 0.66 Km prima di decadere. Il punto è che alla velocità che hanno quando vengono prodotti, l’effetto relativistico fa osservare il decadimento, nel sistema di riferimento del laboratorio a terra, dopo un tempo ![]() ” /> da quando il muone è prodotto, che (a seconda della velocità) è sufficiente a fargli percorrere lo spazio tra l’alta atmosfera e la superficie del pianeta.
” /> da quando il muone è prodotto, che (a seconda della velocità) è sufficiente a fargli percorrere lo spazio tra l’alta atmosfera e la superficie del pianeta.
Ma la Relatività prevede anche altri effetti, perfino più “curiosi”. Riguardo al tempo c’è l’effetto di “redshift gravitazionale”, per il quale la gravità cambia lo scorrere del tempo nei vari punti dello spazio-tempo. Per esempio, mettiamo due orologi a due quote diverse, ma sulla stessa verticale sul nostro pianeta. Trascurando l’effetto di rotazione, e tutti gli altri effetti non puramente gravitazionali, il rapporto tra un intervallo unitario di tempo segnato dai due orologi è
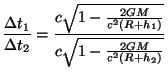 ” />
” />
laddove

Per esempio se uno dei due orologi è posto al livello del mare, e il secondo a 1500 Km di quota, il rapporto differisce da 1 solo alla 10ma cifra decimale. Quindi è un effetto molto piccolo, per quanto comunque misurabile.
Se nel calcolo precedente si tiene anche conto della rotazione terrestre, e si permette agli orologi di muoversi, si ottengono risultati più complicati, come per esempio nel famoso esperimento di Hafele-Keating del 1971 [3].
Invece di misurare il tempo con degli orologi, si possono usare le frequenze dei fotoni emessi da determinati processi fisici, per le quali vale una relazione inversa a quella sopra riportata.
Potremmo applicare il discorso di prima ad un universo arbitrario, popolato da tutti gli oggetti astronomici che vogliamo, e vedere quanto la Gravità influisca sulla misura del tempo proprio nei vari punti. In Astrofisica, per esempio, non potendo dotare di orologi le stelle che si studiano, il loro ruolo viene preso dalle emissioni di fotoni da parte del materiale stellare: siccome è assodato che le Leggi della Fisica laddove sono le stelle che studiamo sono le stesse che abbiamo qui (questa fu una intuizione di Galileo, che molto spesso viene ignorata nella divulgazione, ma che non fu ignorata dall’Inquisizione…) ci basta confrontare le frequenze dei fotoni emessi dalla stella con quelle emesse dagli stessi processi come possiamo misurarli nei laboratori. Possiamo allora per esempio calcolare qual è la distanza che ci separa dalla stella in questione, confrontando il risultato misurato con quello calcolato dal modello di espansione dell’Universo. Questo è il metodo di misura della distanza basato sulla famosa costante di Hubble, e sull’effetto cosiddetto di redshift cosmologico, sul quale non mi dilungo perché è già stato discusso altrove (vedi per es. [4]).
Per cui, anche senza scomodare universi paralleli, è possibile trovare parti del nostro Universo in cui “il tempo scorra diversamente”; ovviamente, è possibile andare oltre (almeno speculativamente) e considerare universi paralleli, in cui essendoci un diverso contenuto di materia, risulti diverso (in intensità) anche il redshift gravitazionale e/o cosmologico.
Se invece si vuole imitare l’esempio dei Grandi della fantascienza, si può fare perfino qualcosa in più, “ritoccando” in un paio di punti le Leggi note della Fisica, e scrivere una storia affascinante, e piacevole da leggere perfino per “gli addetti ai lavori”, come nelle storie di Asimov, Clarke, e Sagan, per esempio.
Vorrei chiudere con una citazione, che non deve indurre a pensare che la Scienza sia un gioco che si gioca meglio senza regole, ma che nella Ricerca bisogna spogliarsi da troppi preconcetti e, in ultima analisi, essere pronti a tutte le sorprese:
“Imagination is more important than knowledge. For knowledge is limited, whereas imagination embraces the entire world, stimulating progress, giving birth to evolution.”
(“L’Immaginazione è più importante della conoscenza. Perché la conoscenza è limitata, mentre l’Immaginazione comprende tutto l’universo, stimolando il progresso, e generando l’evoluzione.”)
Albert Einstein, da "What Life Means to Einstein" in The Saturday Evening Post (26 Ottobre 1929)
Bibliografia
-
- 1
- Isaac Asimov:“Neanche gli Dei”, Urania 608,(1972), Arnoldo Mondadori Editore, ISBN 8804366583
- 2
-
http://www.vialattea.net/esperti/php/risposta.php?num=8175 - 3
-
http://en.wikipedia.org/wiki/Hafele-Keating_experiment - 4
-
http://www.vialattea.net/esperti/php/risposta.php?num=6487