La costruzione di Frank Morley è uno dei più bei risultati di Geometria elementare, tant’è che spesso, in letteratura, si trova anche il termine miracolo di Morley proprio per sottolineare la straordinarietà della proprietà, vera per ogni triangolo piano, già richiamata nel testo della domanda e per la quale riportiamo la seguente figura:
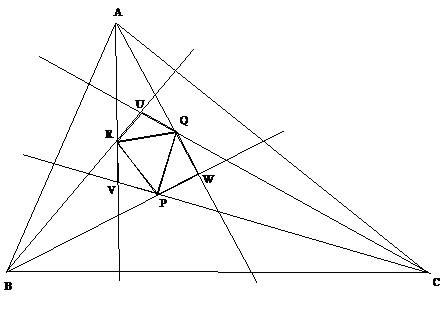
Osserviamo preliminariamente che tale punto è sempre interno a PQR, e quindi anche ad ABC. Se il triangolo ABC fosse ottusangolo, allora il circocentro (centro del cerchio circoscritto=incontro degli assi dei lati) sarebbe esterno ad ABC; ne segue che il circocentro di ABC in generale non è in relazione con il centro di PQR. Una osservazione analoga porta a dire che anche l’ortocentro (incontro tra le altezze) di ABC ottusangolo non ha relazioni evidenti con il centro di PQR, essendo esterna ad ABC una delle sue altezze.
Diverso è invece il discorso a proposito di baricentro ed incentro di ABC; la figura di sopra rende abbastanza evidente che il baricentro di ABC (incontro delle tre mediane) non coincide con il centro di PQR. E’ facile convincersi che la mediana uscente da A non passa per il centro del triangolo PQR (ci vorrebbe una dimostrazione rigorosa, ma la figura è sufficientemente corretta e rende evidente il fatto).
Più delicato è il fatto relativo all’incentro di ABC, ovvero al putno di incontro tra le bisettrici uscenti da A, B e C, che è anche il centro del cerchio inscritto in ABC. Dalla figura infatti potrebbe sembrare che i due punti possano anche coincidere. E’ facile vedere, in generale, che neanche quest’ultimo caso sussiste; infatti (anche qua servirebbe una dimostrazione analitica rigorosa, ma eccessivamente lunga) basta convincersi, osservando varie figure, che, ad esempio, il triangolo ARQ non è isoscele sul lato RQ. La bisettrice uscente da A passerebbe per il centro di PQR solo nel caso in cui il triangolo ARQ fosse isoscele sulla base RQ.
Riassumendo il centro di PQR, in generale, non coincide con nessuno dei punti notevoli del triangolo originario ABC. Le osservazioni di cui sopra sono fondate su figure il più precise possibile. Per avere una dimostrazione rigorosa di ciò è sufficiente, per esempio, coordinatizzare il tutto e trattare la questione dal punto di vista della Geometria analitica; si può fare, anche se diventa alquanto pesante come eccessiva mole di calcolo trigonometrico.