Potreste spiegarmi come si compila un abaco di thorntwaite cioè quello in cui si valuta pioggia, evapotraspirazione reale e teorica ed eccedenza idrica? In tale abaco si devono fare una serie di calcoli e poi ottenere nella colonna della capacità di campo un valore che rimane sempre lo stesso. Però non sò come si usa questo abaco.

Geologia e geografia  ·  Meteorologia e climatologiaViews: 2109
Dalla chiarezza con cui il Lettore ha posto la domanda, si evince che Egli ha già una certa padronanza per lo meno dei principi base dell’idrologia e, nello specifico, del fenomeno dell’evapotraspirazione.
Tuttavia, prima rispondere specificatamente alla Sua richiesta, si ritiene opportuno fare una premessa al fine di rendere l’argomento intellegibile anche a chi non è propriamente della materia.

Di tutta l’acqua presente nel nostro pianeta, i mari e gli oceani ne contengono oltre il 93%. La restante parte è contenuta nelle falde (4,12%), nei ghiaccai (1,65%), nei laghi (0,016%), nei fiumi (0,0001%), nell’atmosfera (0,001%), nel suolo (0,005%).
L’acqua del pianeta Terra è sempre la stessa: essa è soggetta ad un ciclo attraverso cui abbandona gli oceani, torna sui continenti e poi ritorna agli oceani.
Il motore di questo ciclo è l’enegia solare e, per quanto complesso, esso è di seguito schematizzato.

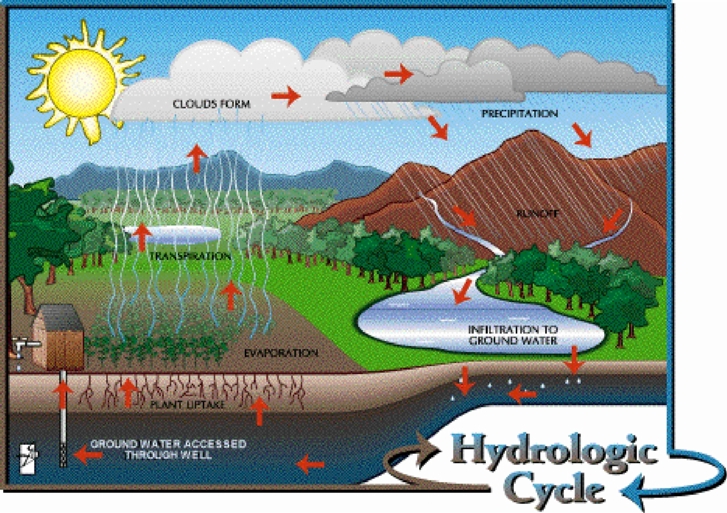
(immagine ripresa da http://www.meteorologia.it/didattica/basico/ciclo%20acqua.htm).

Per evapotrapirazione si intende il passaggio dell’acqua dallo stato liquido allo stato di vapore attraverso l’azione delle piante e del sole.
Essa è di difficile misura. Per questo motivo, nei calcoli dei bilanci idrogeologici, il più delle volte si preferisce stimarla attraverso l’applicazione dei metodi proposti da VV.AA. e di ormai diffuso utilizzo.
Tra questi vi è quello proposto da Thorntwaite.
Questo metodo permette di effettuare il bilancio di un determinato sistema idrogeologico partendo dal confronto dei valori medi mensili di pioggia e di evapotraspirazione potenziale (EP).
Per evapotraspirazione potenziale si intende il quantitativo massimo di acqua che in una certa zona potrebbe evapotraspirare se il suolo fosse sempre umido-bagnato.
Essa si calcola nel seguente modo:

                                EP= 1.6(10 T/I)a c  (cm/mese)

       dove:

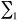I=12 i
 
 i=(T/5)1.514
 
c = fattore di correzione funzione della posizione geografica del bacino (latitudine)
 
T= temperatura media mensile

a=675* 10-9 I3 – 771* 10-7 I2 +1792* 10-5 I+0.49239

 

                                     
 Serra ha semplificato le precedenti formule come di seguito:
 
                                    i=0.09 Tm1.5
                                    a= (1.6 I/100) +0.5

Oltre al concetto di evapotraspirazione potenziale, Thorntwaite introduce quello di capacità di campo del suolo, S, intesa come il quantitativo massimo di acqua che il suolo riesce a trattenere in funzione della sua porosità e del suo spessore.

L’evapotraspirazione reale (ETR) si calcola distinguendo 3 casi:

    Caso 1) P›EP
In questo caso il ETR=EP e la restante parte della pioggia viene assorbita dal terreno fino a raggiungere la sua capacità di campo. Se invece quest’ultima è già stata raggiunta si crea un surplus idrico disponibile all’infiltrazione e al ruscellamento in superficie (eccedenza idrica,Ecc).

    Caso 2) P=EP
Anche in questo caso ETR=EP ma non c’è acqua che si aggiunge a quella già trattenuta dal terreno.

    Caso 3) P‹EP
In questo caso tutto ciò che piove evapotraspira e, inoltre, evapotraspira anche l’acqua trattenuta dal suolo.

Esempio pratico
Supponiamo di voler stimare l’ETR media mensile di un bacino posto alla latitudine di 39°N e con la seguente distribuzione media mensile delle piogge e delle temperature.
Supponiamo di fissare la capacità di campo del suolo, S; in 100 mm.

  T (°C)
P (mm)   c    
 i
  EP
(mm) 		P-EP
(mm)
Ris
(mm)
 ETR
(mm)
 Ecc 
(mm)
 Gen 3 126
0,85
 0,46 
6  120
     
 Feb 4,6 138
0,84
0,88
11
127
     
 Mar 7,1 101
1,03
1,7 
24
77
     
 Apr 11,1 62
1,11
3,34
 47
15
     
 Mag 15,1  51
1,23
5,33
 79
-28
     
 Giu 19,5
14
1,24  7,85 112
-98
     
Lug  22,6
0
1,26
9,81
 139
-39
     
 Ago 22,3  6
1,18
9,62
 128
-122
     
 Set 18,9
47
1,04
7,48
 90
-43
     
 Ott 13,6
139
0,96
4,65
 53
86
     
 Nov 8,7
 203
0,84
2,31
 26
177
     
 Dic 4,9  226
0,82
0,96
 12
214
     
 
Anno
12,6

1113
   
i=54,39
  
727
        
Una volta eseguiti i dovuti calcoli dei parametri poc’anzi esposti, i passi da eseguire sono piuttosto semplici.
Ipotizziamo che nel mese di gennaio le riserve raggiungano il valore massimo (100 mm). Poiché, per questo mese, risulta P-EP›0 allora ETR=EP e la restante parte di pioggia (120 mm) corrisponde all’eccedenza.


  T (°C)
P (mm)   c    
 i
  EP
(mm) 		P-EP
(mm)
Ris
(mm)
 ETR
(mm)
 Ecc 
(mm)
 Gen 3 126
0,85
 0,46 
6  120
100 6
120
 Feb 4,6 138
0,84
0,88
11
127
 100 11
127
 Mar 7,1 101
1,03
1,7 
24
77
100 24
77
 Apr 11,1 62
1,11
3,34
 47
15
100  47
15
 Mag 15,1  51
1,23
5,33
 79
-28
 72 79
0
 Giu 19,5
14
1,24  7,85 112
-98
 0 86
0
Lug  22,6
0
1,26
9,81
 139
-39
 0 0
0
 Ago 22,3  6
1,18
9,62
 128
-122
0
 6
0
 Set 18,9
47
1,04
7,48
 90
-43
0
 47
0
 Ott 13,6
139
0,96
4,65
 53
86
 86 53
0
 Nov 8,7 203
0,84
2,31
 26
177
 100 26
163
 Dic 4,9  226
0,82
0,96
 12
214
 100 12
214
 
Anno
12,6

1113
   
i=54,39
  
727
      
397
716

Procediamo con il bilancio dei mesi successivi.
Fino al mese di aprile valgono le considerazioni fatte sopra.
A partire dal mese di maggio e fino a settembre P-EP assume un valore negativo.
In tal caso, ETR sarà uguale a EP fino a quando le riserve del suolo compenseranno questa differenza.

Ad esempio, a maggio
P= 51 mm
EP= 79 mm
P-EP= -28 mm
ETR=79 mm
Ris= 100-28 =72 mm
Ecc= 0 mm

A giugno il fenomeno dell’evapotraspirazione interesserà tutta l’acqua piovana e prosciugherà del tutto le riserve. Nonostante questo ETR‹EP. L’Ecc. sarà nulla.

Dal mese di ottobre in poi le piogge sono superiori ad EP pertanto ETR=EP. Tuttavia non avremo eccedenza poiché la pioggia “avanzata” alimenterà le riserve fino a che esse arrivino al valore della capacità del suolo.
Questo succede solo in novembre, mese in cui si crea un’Ecc di 163 mm.

All’inizio dell’analisi è stata fatta l’ipotesi che nel mese di gennaio le riserve siano 100.
Procedendo con l’analisi, l’ipotesi fatta in partenza è risultata corretta poiché a gennaio le riserve del suolo non saranno interessate dal fenomeno dell’evapotraspirazione e il loro valore sarà quello massimo. Se così non fosse stato, avremmo contiunuato iterattivamente l’analisi fino a trovare un valore delle riserve del suolo che chiuda la colonna.