Ho ricevuto la sua chiarissima precisazione sul metodo prettamente matematico per manipolare le parametriche e sono già al lavoro. Ho cominciato con l’ellisse che ho fatto ruotare con Evaluate di 360 gradi a Pi/10 per volta, cambiando sempre colore e il risultato oltre che matematicamente utile è anche simpatico graficamente. Utilissima la questione dei due pianeti. Rimane il problema del punto su un cerchio piccolo che rotola o sopra o sotto un cerchio grande. Io ho lavorato un po’ alla bruta tempo fa cercando di controllare, presi dal centro del cerchio grande, seno e coseno. Come avrà capito vado molto ad intuizione anche se desidero molto utilizzare gli strumenti matematici corretti. Tenga conto che sono un pensionato settantenne che ha sempre fatto il chimico. Da qualche anno mi dedico alla matematica alla programmazione e all’utilizzo di MATHEMATICA e MATLAB. Comunque la roto-traslazione non riesco ad applicarla ai casi suddetti. Le invio i miei tentativi fatti con MATHEMATCA che sono corretti ma non fatti con una metodologia convincente.

L’espressione del grafico ricercato dal lettore si costruisce
applicando una opportuna traslazione e fattore di scala all’equazione
parametrica della circonferenza R(cos(t), sin(t)).

Si supponga, senza perdita di generalità
che R=1 e si consideri la Fig. 1.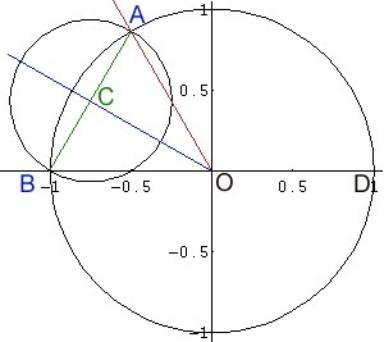

Fig.1:
Costruzione della circonferenza avente per diametro la basedi un poligono
regolare inscritto in una circonferenza unitaria

Si vogliono costruire le n
equazioni delle circonferenze aventi centro C e raggio CB, metà della base del poligono regolare a n lati, inscritto nella circonferenza unitaria.

Inscrivendo un poligono ad n lati in una circonferenza, si ottengono n basi. Si supponga di numerare queste n basi con u parametro k=0,
1, …, n-1.

La fig. 1 mostra la circonferenza g(n,k) costruita sulla base di parametro k=2, dell’esagono regolare (n=6).

Il centro C della
circonferenza g(n,k) da determinare
è il punto medio del segmento AB.

I punti della base AB
si determinano applicando l’equazione della circonferenza unitaria
ai valori degli angoli DOA e
DOB, rispettivamente:

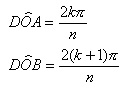
ottenute come multiplo dell’angolo al vertice del poligono
a n lati

da cui l’espressione dei punti A, B

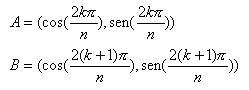
Il centro della circonferenza g(n,k) è dato, quindi, dal punto medio del segmento A,B, ovvero

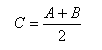
mentre il raggio della circonferenza è pari al seno dell’angolo
AOC (teorema dei seni applicato
al poligono regolare inscritto)

Possiamo quindi applicare la traslazione ed il fattore
di scala adatti all’equazione della circonferenza unitaria per ottenere
g(n,k):

in Mathematica:

p1[n_, k_]:={Cos[2*Pi*k/n],
Sin[2*Pi*k/n]}

p2[n_, k_]:={Cos[2*Pi*(k+1)/n],
Sin[2*Pi*(k+1)/n]}

c[n_, k_]:=(p1[n,k]+p2[n,k])/2

r[n_]:=Sin[Pi/n]

g[n_,k_]:=r[n]*{Cos[a],
Sin[a]}+c[n,k]

ove p1 e p2 corrispondono alle espressioni dei punti
A e B, rispettivamente.

Il tracciamento è ottenuto con l’istruzione

ParametricPlot[{{Cos[a], Sin[a]}, g[6, 2]}, {a, 0, 2*Pi}, AspectRatio->Automatic]

il cui risultato grafico è stato utilizzato come base
per la costruzione della Fig. 1.

Per risolvere il problema posto dal lettore occorre ancora
determinare gli estremi angolari per il tracciamento della circonferenza
g(n,k): abbiamo infatti bisogno di tracciare
n semicirconferenze per coprire
tutta la circonferenza unitaria.

Dalle proprietà geometriche degli angoli, si ottengono
gli estremi angolari

a1[n_, k_]:= Pi/2
+ (k*2*Pi/n+Pi/n)

a2[n_, k_]:=a1[n_,
k_]+Pi

con cui si tracciano gli n
rami del grafico cercato. Tracciando con angoli variabili tra a1[n_, k_] ed a2[n_,k_] si ottengono semicirconferenze
con la convessità rivolta verso l’origine; tracciando con angoli variabili
tra a2[n_,k_] e a1[n_,k_] si ottengono invece le concavità
rivolte verso l’origine.