Premetto che non sono un matematico ma semplicemente un amatore, spero quindi che molte stupidaggini mi saranno perdonate. In particolare mi interessano le curve e la loro origine. Alla equazione parametrica della cicloide ci ero arrivato da tempo ma con un metodo piuttosto farraginoso, la risposta del prof. Consoli in Eureka mi ha dato una dritta per risolvere il problema in modo migliore. Per l’ipo e l’epicicloide applicando la stessa supposizione iniziale fatta dal Prof.Consoli per la cicloide, si arriva alle parametriche ma indubbiamente forzando la mano e affidandosi molto alla intuizione. Può il prof Consoli dare un suggerimento generale di partenza per la derivazione matematica delle curve e ancora più in generale le premesse per derivare le equazioni di un punto di figure geometriche che rotolano dentro o fuori altre figure geometriche, es. un quadrato dentro o fuori un cerchio , oppure se la cosa è molto lunga, partire almeno del rotolamento di figure geometriche su una linea poi si vedrà. La rotazione traslazione degli assi cartesiani può essere una strada ? Chiedo scusa per il disturbo; ma dalle equazioni già fatte da tracciare con Mathematica non traggo grande soddisfazione. P.S. In Mathematica di Stan Wagon il problema è presentato come ovvio ma a dire il vero l’ovvietà non l’ho vista.

Vedi
anche un’altra domanda/risposta sull’argomento

La domanda posta dal lettore è
di grande interesse e spazia nel campo della tecnica di parametrizzazione
delle figure nello spazio euclideo. Una trattazione ampia prevederebbe
un numero di esempi sicuramente non adatto a questa rubrica. In ogni caso,
è possibile definire sinteticamente quali sono le tecniche elementari
che si applicano nel processo di parametrizzazione, dimostrandone graficamente
gli effetti.

Come noto, una curva è identificata
da un sottoinsieme di punti nello spazio bi/tridimensionale, ovvero un
insieme di vettori coppie (x,y) o terne (x,y,z) rispettivamente
nel piano e nello spazio.

Il processo di parametrizzazione
consiste nel definire l’equazione di questi vettori.

La parametrizzazione delle curve
nel piano e nello spazio si ottiene applicando trasformazioni successive
elementari, in modo incrementale.

Si consideri l’equazione parametrica
della circonferenza di raggio unitario e centro (0,0) :

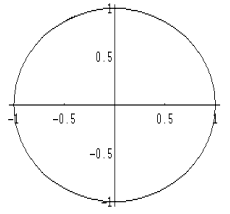
Fig 1: Circonferenza di raggio unitario e centro (0,0)

L’equazione della circonferenza
in Fig. 1 è f(t) = (cos(t), sin(t)), e t è
il parametro.

Il grafico in Mathematica si
ottiene con:

circ[t_] := { Cos[t], Sin[t]};

ParametricPlot[circ[t], {t, 0,
2*Pi}]

Un primo gruppo di trasformazioni
applicabile sono le trasformazioni sul sistema cartesiano di riferimento.

Sia un’equazione f(t) = (x(t),
y(t)) , tali operazioni possono essere:

Fattore di scala: f’(t)
= f(t) *(a,b)^T= (a x(t), b y(t)), con a, b fattori
moltiplicativi costanti.
Traslazione: f’(t) = f(t)
– (a, b) = (x(t) – a, y(t) – b), con a,b costanti
additive.
Rotazione: f’(t) = r(w) *
f(t)^T=r(w) * (x(t) , y(t))^T = (x(t) cos(w) – y(t)
sin(w), y(t) cos(w) + x(t) sin(w)),

ove w è l’angolo
di rotazione e r(w) è la matrice di rotazione

Si osservi che si indica con [*]
il prodotto matriciale, il Mathematica supporta il prodotto
matriciale con l’operatore [.]. L’apice ‘T’ indica trasposizione,
ovvero l’operazione di scambio righe/colonne di una matrice, il Mathematica
supporta la trasposizione mediante la funzione Transpose[].
Queste operazioni non possono essere definite qui nel dettaglio, si veda
in proposito un qualsiasi testo di Algebra Lineare.

Applichiamo ora la trasformazione
1 per applicare un fattore di scala 2 alle ascisse e 3 alle
ordinate:

f’(t) = (2 cos(t), 3 sin(t))

In Mathematica:

ell1[t_] := { 2 Cos[t], 3 Sin[t]};

ParametricPlot[ell1[t], {t, 0,
2*Pi}]

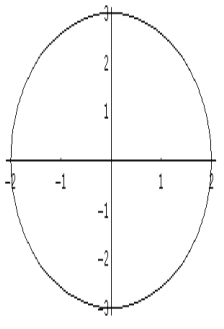
Fig 2: Ellisse di
centro (0,0) ed assi 4 e 6

Quale luogo geometrico abbiamo ottenuto
?

Allungando di un fattore 2 e 3 rispettivamente
le ascisse e le ordinate, abbiamo ottenuto l’equazione parametrica un
ellisse con asse maggiore 4 ed asse minore 6.

Applichiamo la seconda e la terza
trasformazione all’ellisse di Figura 2 e spostiamone l’origine in (2,3),
ruotandola di 45° (vale a dire di p /4). Applichiamo prima una rotazione:

f’(t) = r(w)*(x(t),
y(t))^T = (x(t) cos(w) – y(t) sin(w), y(t) cos(w) + x(t) sin(w))
=

=(2 cos(t) cos(w)
– 3 sin(t) sin(w), 3 cos(w) sin(t) + 2 cos(t) sin(w))

e poi la traslazione, aggiungendo
(2,3):

(2,3) + r(w)*(x(t),
y(t))^T =

=(2+2 cos(t) cos(w)
– 3 sin(t) sin(w), 3+3 cos(w) sin(t) + 2 cos(t) sin(w))

ove w = p /4.

La serie di trasformazioni si definisce
in Mathematica in modo molto semplice:

x[t_] := (2*Cos[t]);

y[t_] := (3*Sin[t]);

r[w_] := {{Cos[w], -Sin[w]},
{Sin[w], Cos[w]}};

ell2[t_] := { {2,3}+r[Pi/4].
Transpose[{x[t], y[t]}] }

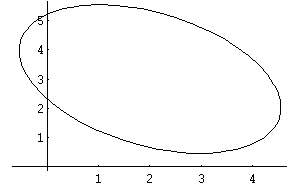
Fig. 3: Ellisse di
Fig. 2 ruotata di 45° e traslata in (2,3)

Queste operazioni elementari, consentono
di trasformare le curve nel piano e nello spazio a piacimento.

Applichiamo ad esempio l’ingrandimento
in scala per ottenere l’equazione parametrica di una spirale:

spir[t_] := t*{ Cos[t], Sin[t]};

ParametricPlot[spir[t], {t, 0,
24*Pi}]

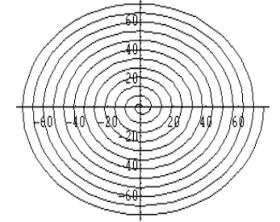
Fig 4: Spirale piana

La spirale piana di Fig. 4 si ottiene
applicando un fattore di scala variabile e proporzionale all’angolo di
rotazione.

Cosa succederebbe se invece traslassimo
la circonferenza nello spazio, verso l’alto, mentre questa viene generata
? La risposta è in Fig. 5.

spir3D[t_] := { Cos[t], Sin[t],
t/7};

ParametricPlot3D[spir3D[t],
{t, 0, 6*Pi}]

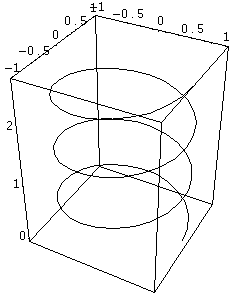
Fig
5: Spirale cilindirica

La spirale cilindrica di figura
5 è ottenuta traslando la circonferenza verso l’alto con velocità
t/7.

Quali operazioni elementari sono
state applicate per ottenere le parametrizzazioni di figura 4 e 5 ?

A proposito dell’epicicloide (la
curva descritta dai pianeti esterni del sistema solare vista dalla terra);
sia l’equazione (supponiamo circolare) dell’orbita di due pianeti (cos(8t),
sin(8t)) e (2 cos(t), 2 sin(t))

p1[t_] := {Cos[8 t], Sin[8 t]};

p2[t_] := {2 Cos[t], 2 Sin[t]};

ParametricPlot[p2[t]-p1[t], {t,
0, 4 Pi}]

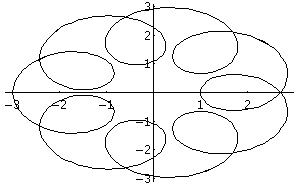
Fig 6: Epicicloide

Il pianeta interno compie 8 orbite
e quello esterno solo una, il diametro di orbita del pianeta esterno è
il doppio di quello interno. L’orbita del pianeta esterno “vista”
da quello interno si ottiene semplicemente impostando l’origine del sistema
cartesiano di riferimento al luogo dei punti dell’orbita interna. In poche
parole: sottraendo l’equazione dell’orbita interna a quella esterna. Il
risultato è in fig. 6.

Possiamo spingerci ancora oltre
nel processo di parametrizzazione e costruire delle superfici a partire
da curve nel piano. Ciò che distingue una curva da una superficie
è il numero di parametri: 1 per le curve e 2 per le superfici.

In particolare, esiste un procedimento
standard per costruire una superficie di rotazione, a partire da
una curva nel piano, che consiste nell’aggiungere un parametro apposito,
applicando la rotazione della curva nello spazio.

Si consideri lo spazio tridimensionale
e si supponga di avere una curva nel piano XOZ, ad esempio la parabola
(x, y, z) = (t, 0, t²) :

ParametricPlot3D[{t , 0 , t^2},
{t, -1, 1}]

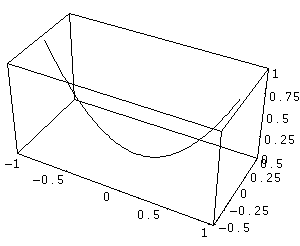
Fig 7: Parabola nel piano XOZ

Applichiamo ora la trasformazione
di coordinate seguente; sia f(t) = (x(t), 0, z(t)) la curva nel
piano XOZ da ruotare:

Rotazione sull’asse Z: f’(t)
= (x(t) cos(u), x(t) sin(u), z(t))

ove si aggiunge un parametro addizionale
u di rotazione.

Applichiamo alla parabola di fig.
7:

f’(t) = (t cos(u),
t sin(u), t²)

ParametricPlot3D[{t Cos[u], t
Sin[u], t^2}, {t, 0,1}, {u, 0, 2*Pi}]

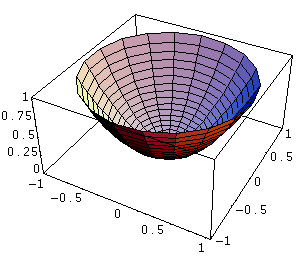
Fig
8: Paraboloide

Il risultato è illustrato
in Fig. 8.

Prendiamo ora la circonferenza nel piano XOZ (3+cos(t), 0, sin(t))
di raggio 1 e centrata in (3,0,0):

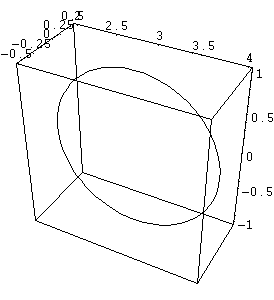
Fig. 9: Circonferenza
nel piano XOZ di raggio 1 e centro (3,0,0)

Applichiamo la rotazione:

f’(t) = ((3+cos(t)) cos(u), (3+cos(t))
sin(u), sin(t))

ParametricPlot3D[{(3+Cos[t])
Cos[u], (3+Cos[t]) Sin[u], Sin[t]}, {t, 0,2 Pi}, {u, 0, 2*Pi}]

Il risultato è il toro
di fig 10.

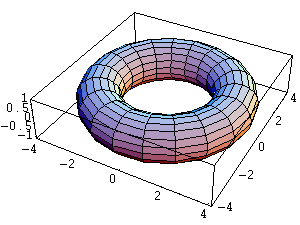
Fig 10: Toro