D:
La formula di Erone è uno degli esempi più
brillanti di applicazione delle proprietà geometriche dei triangoli.
Formula di Erone:
![]()
ove s è il semiperimetro del triangolo e a, b,
c le misure dei suoi lati.
Alla dimostrazione geometrica, dovuta allo stesso Erone,
è difficile aggiungere altro.
In questa sede, aggiungiamo unicamente qualche commento
all’ottimo lavoro presente all’indirizzo
http://galileoandeinstein.physics.virginia.edu/more_stuff/Heron.html
che presenta la dimostrazione geometrica “canonica”.
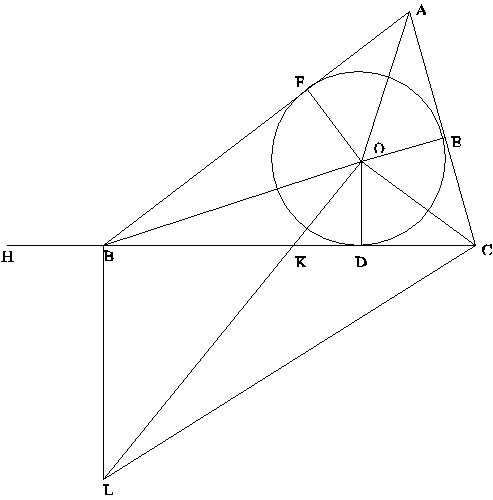
Si osservi la circonferenza inscritta.
Per il teorema delle tangenti da un punto esterno ad una
cironferenza, sussistono le seguenti relazioni di uguaglianza tra segmenti:
AF=AE
BF=BD [1]
CE=CD
Inoltre,
OF=OE=OD [2]
perché raggio della circonferenza inscritta.
Si osservi che, per le proprietà della circonferenza
inscritta in un triangolo, i segmenti CO, AO, BO giacciono sulle bisettrici
degli angoli DOE, EOF, DOF, per cui sussistono le ulteriori uguaglianze
tra angoli:
DOC = COE
DOB = BOF [2a]
FOA = EOA
Altra proprietà:
AFO, CEO, CDO sono angoli retti [3]
Ora, siano a, b, c le lunghezze dei tre lati, l’area del
triangolo ABC è pari al perimetro p=a+b+c per il raggio della circonferenza
inscritta:
a(ABC) = p OD [4]
Si estenda ora il lato CB per una porzione di segmento
BH=AF.
Per le proprietà [1], si ottiene
CH = p/2 [5]
che, sostituita alla [4], da
a(ABC) 2 = CH2OD2 [6]
L’idea è di ricavare la tesi proprio da questa
espressione, e lo strumento per farlo è la similitudine dei triangoli.
Si traccino infatti i segmenti BL e OL in modo che gli
angoli CBL, COL siano retti.
Applicando le proprietà di uguaglianza degli angoli
[2a] e tenendo conto degli angoli retti [3] e di quelli ottenuti per costruzione
(COL e CBL), si ottiene l’uguaglianza tra angoli
AOF = CLB [7]
(questo passaggio è estremamente delicato e lungo,
per convincersi della [7] si consiglia di tracciare a matita tutti gli
angoli uguali ottenuti per calcolo – tenendo presente che la somma degli
angoli di un triangolo è 180 gradi – sfruttando le relazioni note
tra gli angoli [2a] e [3] ).
La [7] implica, quindi, la similitudine dei triangoli
AOF e CLB, retti per la proprietà [3].
Ricordiamo che due triangoli sono simili se godono delle
proprietà (ciascuna è condizione necessaria e sufficiente
e le due si implicano vicendevolmente):
- Hanno gli stessi angoli.
- I loro lati sono proprorzionali.
da cui, per costruzione, essendo BH=AF e per la similitudine
dei triangoli AOF e CLB si ottengono le proporzioni che seguono:
BC:BL = AF:FO = BH:OD [8]
CB:BH = BL:OD = BK:KD [9]
essendo inoltre, per costruzione e per le proprietà
[1]
CB:BH = CH:HB [10]
da cui si ottiene, combinando la [10] e la [9]:
CH:HB = BD:DK [11]
a questo punto si ottiene la tesi combinando la [8], [9],
[10] e [11] in:
CH2: (CH HB) = (BD DC): (CD
DK) [12]
ma, applicando il II teorema di Euclide sul triangolo
COK, retto per costruzione, si ottiene
CD DK = OD2 [13]
e, quindi:
CH2: (CH HB) = (BD DC):(CD DK)
= (BD DC):OD2 [14]
A questo punto sfruttiamo la [6] per scrivere la relazione
a(ABC)2 = CH2 OD2
= CH HB BD DC [15]
e, ponendo s = CH=p/2 (proprietà [5] ), otteniamo
il quadrato dell’area del triangolo ABC
a(ABC)2 = CH2 OD2
= CH HB BD DC = s(s-a)(s-b)(s-c).
Una nota ulteriore:
la formula di Erone può essere applicata ai quadrilateri
in particolare ed ai poligoni irregolari in generale scomponendoli in
triangoli. Ciascuna area dei triangoli ricavati può essere, quindi,
ricavata separatamente mediante la formula dimostrata.