La domanda è un po’ oscura e, probabilmente,
l’essenza della domanda sta nella sua indefinitezza:
il lettore non ha chiari i concetti di limite e
continuità.
Riepiloghiamo brevemente le definizioni che
coinvolgono gli oggetti trattati.
Intervallo
- I intervallo chiuso di centro x0
e raggio d :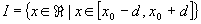
- I intervallo aperto di centro x0
e raggio d :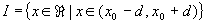
Un intervallo è detto chiuso se contiene gli
estremi, aperto se non li contiene. Un intervallo
può contenere “buchi”, ad esempio essendo
definito privo del proprio punto centrale.
Punto di accumulazione
- x0 è punto di
accumulazione se ogni intervallo I di
centro x0 contiene
infiniti punti
Il concetto di punto di accumulazione è uno strumento
per studiare il comportamento delle funzioni in un
intorno infinitamente piccolo di un punto. Affermare che
un punto è di accumulazione significa assicurarsi
l’esistenza di tutti i punti infinitamente vicini a
quel punto e, quindi, di poter operare su di essi.
Limite di funzione
Siano:
- f una funzione dai reali ai reali
- x0 punto di
accumulazione - I(x0, d)=
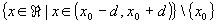
intervallo aperto con centro in x0 e
raggio d, privo del punto x0
Diciamo che f tende al limite l in x0,
se e solo se
ed indichiamo questa proprietà con la notazione: ![]() .
.
Ovvero la funzione f tende ad l in un
suo punto di accumulazione x0
quando, per ogni e positivo e
piccolo a piacere, esiste un d altrettanto piccolo, ma funzione di e, tale che la funzione f calcolata
in punti prelevati da un intervallo di centro x0
e raggio d assume
valori che differiscono da l per una quantità
minore di e.
I limiti destro e sinistro vengono
definiti semplicemente utilizzando rispettivamente gli
intorni destro e sinistro del punto di accumulazione.
Diciamo che f tende al limite l in x0,
da destra se e solo se
ed indichiamo questa proprietà con la notazione (limite
destro): ![]() .
.
Diciamo che f tende al limite l in x0,
da sinistra se e solo se
ed indichiamo questa proprietà con la notazione (limite
sinistro): ![]() .
.
Il limite se esiste deve essere unico, e ciò implica
la coincidenza dei limiti destro e sinistro, ovvero
![]()
Continuità di funzione
- f è continua in I se
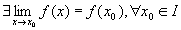
Una funzione è quindi continua in un punto se il
limite in quel punto, che deve essere di accumulazione
perché il limite esista, è pari al valore della
funzione nel punto stesso.
Per concludere, il concetto di punto di accumulazione
è utile per definire una proprietà senza la quale le
operazioni di limite e, quindi, lo stesso concetto di
continuità non avrebbero senso. Il punto di
accumulazione è nato, quindi, per investigare
l’andamento di funzioni in intorni di punti di
grandezza infinitamente piccola.