Lo si è stabilito studiando il moto della Luna, usata in questo caso come orologio naturale che segna il tempo delle effemeridi.
Nel 1967 la tredicesima conferenza generale dei pesi e delle misure definì il secondo come
la durata di 9.192.631.770 periodi della radiazione corrispondente alla transizione tra due livelli iperfini dello stato fondamentale dell’atomo di cesio 133
Nel 1997 si è precisato che la definizione si riferisce all’atomo di cesio a riposo e alla temperatura di 0 K.
Già dal 1956 il Comitato Internazionale dei pesi e delle misure aveva definito il secondo in termini di secondo delle effemeridi.
Il secondo è la frazione 1 / 31.556.925,9747 dell’anno tropico, per il giorno 0 gennaio 1900, alle ore 12 del tempo delle Effemeridi.
Il tempo delle effemeridi è quello scandito dal moto della Terra attorno al sole, quasi si trattasse di un immenso orologio naturale. In sostanza è il tempo che rende vere le equazioni della dinamica newtoniana.
Nella pratica però non si usa il moto della Terra attorno al Sole, perché occorrerebbe rilevare l’esatta posizione del Sole rispetto alle stelle, cosa impossibile. Dunque si usa il moto della Luna attorno alla Terra, anche in virtù della maggiore rapidità che consente una maggiore precisione. La teoria del moto orbitale permette di stabilire la posizione della Luna in funzione del tempo, se invece si vuole operare in senso inverso, vale a dire conoscere il tempo in funzione della posizione, occorre misurare con estrema precisione la posizione della Luna rispetto alle stelle.
Ciò si realizza per mezzo della fotografia: si misura la posizione del centro del disco lunare rispetto alle stelle di campo. Il problema però sta a monte: nel realizzare la fotografia.
 Questa operazione non è semplicissima, in primo luogo perché il
Questa operazione non è semplicissima, in primo luogo perché il
nostro satellite è molto più brillante delle stelle, dunque il tempo di esposizione della lastra fotografica non può essere adeguato sia per le stelle che per la Luna. In secondo luogo per ottenere una buona fotografia occorre un tempo di posa dell’ordine delle decine di secondi e in questo lasso di tempo la Luna si sposta apprezzabilmente
nel cielo!
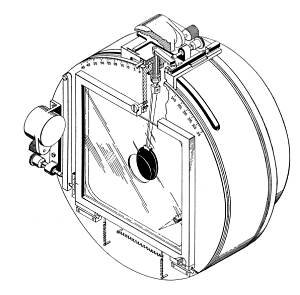
La soluzione è stata trovata da W. Markowitz che ha costruito una camera a doppia velocità (illustrata a fianco) da applicare ad un telescopio.
Il motorino visibile a sinistra fa scorrere la lastra fotografica in modo da inseguire lo spostamento delle stelle. Il disco nero è in realtà un filtro lunare che lascia passare solo l’uno per mille della luce incidente, in modo tale da eguagliare lo splendore delle stelle. Inoltre il meccanismo in alto fa ruotare il filtro in modo da compensare lo spostamento della Luna rispetto alle stelle. Il risultato è una fotografia, con un tempo di posa di 20 secondi, che ritrae la Luna perfettamente fissa in un campo stellare.
Come facciamo a sapere a quale istante si riferisce questa situazione?
Del resto la posa e’ durata ben 20 secondi…
La risposta è data da un piccolo contatto elettrico posto nel gruppo di meccanismi in alto. Quando il filtro è perfettamente parallelo alla lastra, l’immagine della Luna non viene spostata rispetto alle stelle, dunque l’intera fotografia rappresenta quell’istante di tempo. Il contatto è collegato ad un cronografo che registra il tempo esatto dell’osservazione.
La descrizione di questa apparecchiatura e del metodo di lavoro è stata data in un articolo1 del 1954, ma già dal 1952 allo U.S. Naval Observatory Markowitz aveva iniziato a rapportare il moto della Luna al tempo delle effemeridi. Dal giugno 1955 al 1958 una collaborazione anglo-americana ha studiato a fondo il moto della Luna in rapporto al tempo marcato dagli orologi atomici. L’articolo finale2 dà come risultato il rapporto tra il secondo di tempo delle effemeridi rispetto alla radiazione emessa dal cesio: 9.192.631.770 +/- 20 cicli.
Note:
1 – W. Markowitz, Photographic determination of the Moon’s position, and applications to the measure of time, rotation of the Earth, and geodesy, Astron. J. 59, 69 (1954)
2 – W. Markowitz, R. Glenn Hall, L. Essen, J. Parry, Frequency of cesium in terms of ephemeris time, Phys. Rev. Letters, 1, 105 (1958).
Vedi anche la risposta alla richiesta di precisazioni.