Una precisazione preliminare: la Luna, come ogni altro oggetto sulla sfera celeste, al suo sorgere ha altezza = 0 ma non necessariamente declinazione = 0: i due concetti coincidono solo ai poli terrestri, dato che la declinazione è l’altezza di un oggetto sull’equatore celeste.
Vediamo al nucleo della domanda.
Quello del moto della Luna è un problema estremamente complesso, in cui entrano in gioco molti fattori di meccanica celeste. Di conseguenza riuscire a “figurarsi” le caratteristiche principali credo sia un’operazione quasi impossibile.
Possiamo però fare alcune semplificazioni, vedendo di trarre alcune regole generali.
Partiamo da un problema molto più semplice, cioè quello del Sole.
Guardando questa precedente risposta si può vedere che, nota la declinazione di un oggetto sulla sfera celeste e la latitudine del luogo, è possibile ricavare l’azimuth al sorgere con una semplice formula trigonometrica.
Ora, fissiamo per comodità la latitudine ad un valore di circa 45° nord, ed esaminiamo come varia l’azimut del Sole al suo sorgere nel corso dell’anno. Per semplificare un po’ le cose, supponiamo l’orbita terrestre circolare, nel qual caso il Sole compie un moto uniforme lungo l’eclittica. Dato che l’eclittica è inclinata di 23° 27′ rispetto all’equatore celeste, ciò equivale a dire che la declinazione del Sole nel corso dell’anno varia sinusoidalmente con un periodo appunto di un anno e ampiezza pari al valore dell’inclinazione.
Quello che ci aspettiamo dunque è che l’azimuth del Sole vari con andamento periodico tra un minimo che si ha al solstizio d’estate, calcolabile con le formule citate ponendo la declinazione pari a +23.45 gradi, e un massimo al solstizio d’inverno, per la declinazione pari a -23.45 gradi.
Nella figura seguente è riportato l’azimuth del Sole al suo sorgere per le coordinate di Milano, nel corso dell’anno 2005.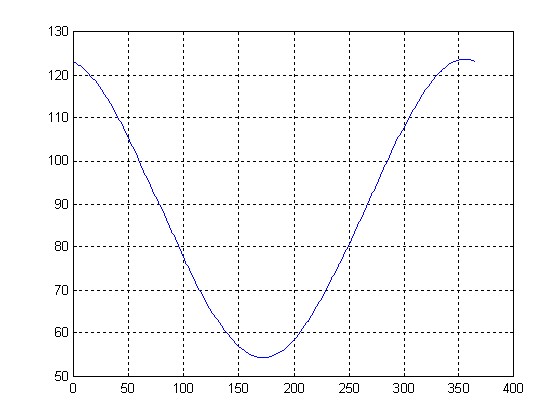
Passiamo ora alla Luna.
Come prima brutale approssimazione, supponiamo che essa abbia un’orbita circolare, complanare con l’eclittica. In questo caso, si tratterebbe semplicemente di un corpo celeste che percorre la medesima orbita apparente del Sole, semplicemente ad una velocità circa 13 volte maggiore. Quello che ci possiamo aspettare è dunque che, nel corso dell’anno, la posizione dell’azimuth al sorgere ripercorra un andamento simile a quello del Sole, semplicemente con una periodicità più rapida.
Nella figura seguente è riportato l’azimuth del sorgere della Luna, sempre per Milano, nel corso del 2005, e come si vede l’approssimazione è abbastanza buona.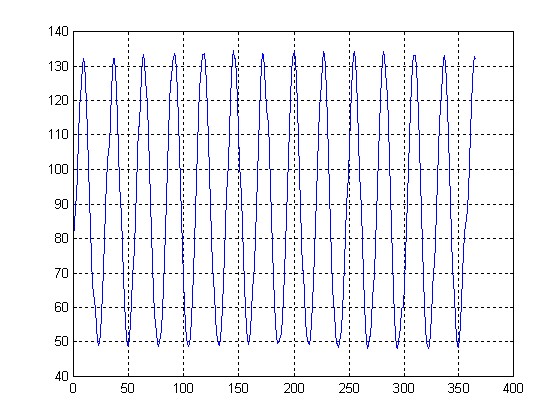
Introduciamo ora un primo fattore di correzione: a causa del suo periodo siderale piuttosto breve (circa 28 giorni), la Luna ha un moto proprio molto elevato. Dobbiamo pensare che, quando calcoliamo il suo azimuth al momento in cui sorge, non facciamo altro che “campionare” la declinazione della Luna circa una volta al giorno, e usare la sua declinazione in quel momento per calcolare l’azimuth. Siccome il nostro periodo di campionamento è piuttosto grande rispetto al periodo del fenomeno, si introducono fenomeni di “battimento”.
Guardando il grafico, infatti, si vede che i punti di azimuth massimo e minimo non sono costanti ma hanno una debole oscillazione sovrapposta. Si può immaginare il fenomeno in questo modo: quando la Luna raggiunge la massima o minima declinazione, se siamo in prossimità dell’istante in cui sorge campioneremo in effetti l’azimuth minimo o massimo, se invece in quel momento sta tramontando, dovrà passare ancora circa mezza giornata prima del suo sorgere, e nel frattempo la sua declinazione si sarà sensibilmente spostata dai punti di massimo o minimo assoluti.
Come secondo fattore correttivo introduciamo l’inclinazione dell’orbita lunare. Come noto l’orbita della Luna non è complanare con quella apparente del Sole, ma è inclinata di circa 5.1° sull’eclittica. Inoltre i punti in cui i due piani orbitali si intersecano (detti nodi lunari) non sono costanti nello spazio, ma ruotano con un periodo di circa 18 anni, che è detto Saros.
Se immaginiamo che i nodi siano fissi, l’effetto dell’inclinazione dell’orbita lunare è quello di introdurre un’ulteriore oscillazione nella declinazione, con ampiezza di 5 gradi. Quando i due nodi sono circa allineati con i punti equinoziali, ed il nodo ascendente della luna coincide con il punto equinoziale di primavera (che è il nodo ascendente del Sole), in sostanza la correzione di 5° si va a sommare all’oscillazione di 23° dovuta al moto lungo l’eclittica, avendo come risultato che la Luna percorre un’orbita molto più inclinata. Di conseguenza l’azimuth al suo sorgere può variare di più di quello del Sole. Quando, circa 9 anni dopo, i nodi si sono invertiti, l’inclinazione dell’orbita lunare si sottrae invece a quella eclittica, per cui l’azimuth della Luna tende a variare meno. Ovviamente nel corso di un Saros, si ottengono anche tutte le situazioni intermedie.
Nella figura seguente è indicato con ogni puntino l’azimuth della Luna al sorgere per Milano, a partire dal 1 gennaio 2005 e per i 18 anni successivi. Come si vede, tra il 2005 e il 2006 siamo nella situazione vicina all’allineamento dei nodi, in cui l’inclinazione dell’orbita lunare si somma a quella dell’eclittica. In questa situazione si raggiungono l’azimuth massimo, in corrispondenza di una declinazione di circa 28.5° (23.45 + 5.1) e minimo, per declinazione -28.5°. Dopo 9 anni la situazione si inverte, e l’oscillazione dell’azimuth ha l’ampiezza minima, dato che la declinazione della Luna può variare solo tra +18.5° (23.45 – 5.1) e -18.5°.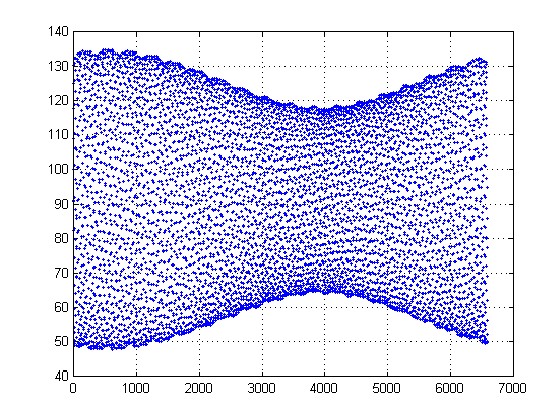
Naturalmente quella descritta è una situazione semplificata, in cui si tiene conto solo degli effetti principali. Per un calcolo esatto si dovrebbe tenere conto dell’ellitticità dell’orbita lunare, della parallasse della Luna rispetto all’osservatore, della nutazione, ecc…
Per tracciare i grafici sopra riportati, mi sono servito delle routine scritte in Matlab dal dott.Eran Ofek, che ringrazio. Esse sono gratuitamente scaricabili presso il suo sito, all’indirizzo http://wise-obs.tau.ac.il/~eran/matlab.html