 Se
Se
prendiamo come piano di riferimento l’equatore celeste, l’eclittica ha
un’inclinazione rispetto ad esso di circa 23°,5 l’equatore galattico
è inclinato di circa 62°.
L’angolo che formano eclittica ed equatore galattico (prese entrambe con
il verso positivo nella direzione in cui la rispettiva longitudine cresce
e muovendosi dall’eclittica verso l’equatore) è di -60° (cioè mi muovo
in senso orario).
Per conoscere
l’inclinazione dell’eclittica rispetto all’equatore galattico non è
sufficiente calcolare la differenza tra 62° e 23° perché
i tre cerchi massimi non si intersecano nel medesimo punto!
Come
si vede dalla figura seguente, i due piani si intersecano quasi esattamente
a a 90°,0 e a 270°,0 di longitudine eclittica (e ovviamente a 0° di latitudine).
In coordinate equatoriali i punti di intersezione si trovano a circa 18h00m;
-23°27′ e l’altro a 6h00m; +23°27′.
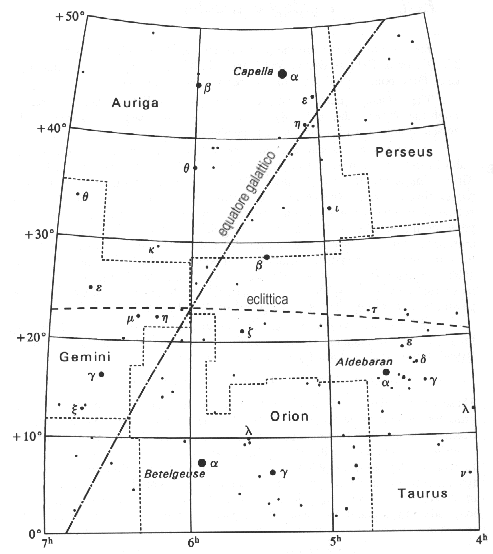
E’ curioso notare che l’intersezione del piano galattico con l’eclittica
avviene proprio in coincidenza dei punti di massima elongazione nord e
sud dell’eclittica sull’equatore celeste, vale a dire nei punti corrispondenti
ai solstizi! In realtà a causa della precessione degli equinozi
la coincidenza è passeggera, a dire il vero l’esatta sovrapposizione
dell’equatore galattico con i punti solstiziali si è avuta nel
Maggio 1998.
Gli abitanti
dell’emisfero australe vedono meglio la parte centrale della Via Lattea
perché il centro galattico ha una declinazione di circa -30°.
La formula che ci fornisce l’altezza sull’orizzonte di un oggetto celeste
è
![]()
dove
![]() è la latitudine
è la latitudine
del luogo di osservazione (ricordo che la latitudine per le località
dell’emisfero boreale è negativa) e ![]()
è la declinazione dell’oggetto celeste. In particolare, per il
centro galattico abbiamo h = 60° – ![]() .
.
Alla latitudine di 30°S possiamo avere l’imponente visione del centro
galattico allo zenith, con la scia della via lattea che attraversa tutta
la volta celeste!
Un commento
I commenti sono chiusi.