La principale difficolta’ di questo metodo consiste nella determinazione del meridiano locale. E’ da scartare assolutamente l’uso della bussola, perché anche conoscendo la declinazione magnetica per la località in cui ci si trova, ci possono essere disturbi notevoli (campi elettromagnetici, metalli, ecc.). Possiamo pensare, ad esempio, di seguire l’ombra proiettata da un’asta (gnomone) e determinare il punto in cui essa è più corta: la retta individuata da quel punto e la base dell’asta sarà il meridiano locale.
L’equazione del tempo descrive lo scarto di tempo tra il passaggio in meridiano del Sole vero rispetto al Sole medio (un Sole fittizio che va a definire il tempo segnato dai nostri orologi). Se ad esempio supponiamo di eseguire questo esperimento il 15 gennaio, dall’almanacco astronomico leggiamo che l’equazione del tempo è di -9m13s, e dunque il Sole vero sarà in ritardo sull’ora indicata dai nostri orologi (cioè a Greenwich transiterà in meridiano dopo mezzogiorno).
N.B. Si faccia attenzione alle diverse convenzioni: alcuni almanacchi riportano l’equazione del tempo col segno cambiato !!
Ad esempio dall’esperimento eseguito il giorno 15 gennaio 2000 rileviamo che il Sole raggiunge il meridiano locale alle ore 12h30m37s segnate dal nostro orologio.
Dato che a gennaio è in vigore l’ora solare, l’ora di Greenwich corrispondente sarà 11h30m37s.
Lo scarto tra il mezzogiorno e l’ora effettiva di culminazione del Sole è dunque di 29m23s, i quali sono dovuti sia alla differenza in longitudine con Greenwich, che al ritardo tra Sole vero e Sole medio.
Per quest’ultimo effetto occorre fare attenzione al segno: nel nostro caso il segno meno nell’equazione del tempo ci dice che il Sole vero è in ritardo sul Sole medio e dunque dobbiamo sommare il ritardo precedentemente ottenuto con il valore dell’equazione del tempo per quel giorno.
Sarà utile un semplice disegno: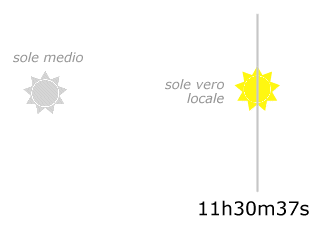
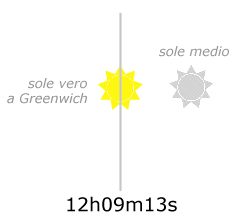
Vediamo che il Sole medio nella situazione locale e quello a Greenwich “distano” (12h00m00s-11h30m37s)+09m13s.
Dunque alla differenza di longitudine sono imputabili 38m36s, e per convertire il tempo in longitudine occore moltiplicare per il rapporto tra 360° e la durata di un giorno siderale.
Il fattore di conversione è molto vicino a 4 minuti, perciò il nostro scarto in longitudine sarà di 9°39′.
Per quanto riguarda la precisione, si noti che un errore di 4 secondi sulla determinazione del tempo di culminazione o sul valore dell’equazione del tempo comporta un errore di 1′ in longitudine.