Nota:
la risposta rigorosa richiede troppi passaggi matematici, per cui in questa
sede tratteremo in modo intuitivo il problema della navigazione spaziale.
 Immaginiamo
Immaginiamo
di trovarci ai comandi di una potentissima astronave: intorno a noi si
trovano i pianeti del sistema solare. Se ad esempio vogliamo andare su
Marte, viene istintivo individuare il pianeta, puntare l’astronave nella
sua direzione e mettere i motori al massimo, così come in bicicletta per
spostarci dobbiamo semplicemente dirigerci verso l’obiettivo e pedalare.
Tuttavia in questo modo mancheremmo clamorosamente il pianeta e ci perderemmo
nello spazio interstellare. Questo perché il nostro modo di concepire
il movimento è limitato al mondo terrestre.
Nello spazio
vale il principio di inerzia: vale a dire che spegnendo i motori,
con nostra grande sorpresa, l’astronave non si fermerebbe a poco a poco,
ma continuerebbe la sua folle corsa con la stessa velocità che possedeva
un attimo prima di spegnere i motori! Inoltre l’attrazione gravitazionale
del Sole e dei pianeti fa sì che l’astronave non segua mai una traiettoria
rettilinea, ma curva. Per questi motivi la navigazione spaziale è una
scienza piuttosto complicata.
Vediamo
qualche idea su come si può guidare un veicolo spaziale: per comodità
consideriamo un satellite nel campo gravitazionale terrestre. L’equazione
fondamentale del moto è la seguente:
![]()
A sinistra
compaiono due forze: la forza gravitazionale, originata dalla Terra, e
la spinta dei razzi del veicolo. A destra la consueta espressione della
seconda legge di Newton. In linea di principio possiamo far percorrere
al satellite qualsiasi traiettoria, purché la spinta S sia molto grande,
tanto da rendere trascurabile la forza gravitazionale. Se così fosse potremmo
procedere a zig-zag, oppure descrivere traiettorie stranissime, insomma
fare come ci piace. Purtroppo non è così perché la spinta che possiamo
applicare ad un veicolo spaziale è limitata enormemente da questioni di
costo: ogni chilogrammo di combustibile prima di rendersi utile fornendo
una spinta è un peso morto, che il veicolo deve trascinare con sé.
Possiamo
però fare una considerazione furba: i pianeti descrivono le loro orbite
senza l’impego di carburante, perché è la forza gravitazionale a determinare
l’orbita. Dunque possiamo semplicemente lasciare il satellite in balìa
della gravità, che “guiderà” il satellite lungo la sua orbita, lasciando
all’intervento umano (o meglio dei razzi) il solo compito di scegliere
quale orbita percorrere. A livello di aneddoto, durante una delle
missioni
Apollo, il figlioletto di un astronauta, durante il collegamento con
il padre in viaggio verso la Luna, chiese chi stava guidando l’astronave,
ed il padre rispose semplicemente “Newton”. Questa risposta è azzeccatissima,
perché in realtà l’uomo non faceva proprio nulla, si lasciava trasportare
dalla forza che il
grande scienziato inglese aveva scoperto.
Dunque esiste
una serie di traiettorie che chiameremo per essere chiari traiettorie
gratis. E dunque il problema della navigazione spaziale è il seguente:
sfruttare le “traiettorie gratis” al meglio, bruciando combustibile solo
per trasferirsi da una traiettoria gratis ad un’altra. Le traiettorie
gratis sono tutte le coniche, ovvero: la circonferenza, l’ellisse,
la parabola e l’iperbole.
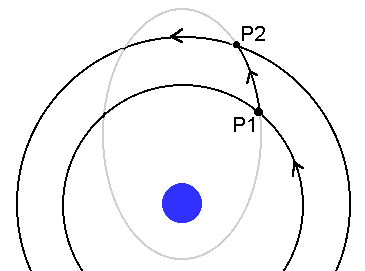 Consideriamo
Consideriamo
il seguente problema: trasferire un satellite dall’orbita interna circolare
a quella più esterna concentrica.Come
orbita di trasferimento scegliamo l’ellisse grigia. Dato che l’orbita
ellittica è “gratis”, dovremo accendere i razzi in P1 per trasferire il
veicolo sull’orbita ellittica, viaggeremo da P1 a P2 senza consumare carburante,
ed infine giunti in P2 accenderemo i razzi per trasferire il veicolo sull’orbita
circolare, che percorreremo senza consumo di carburante.
Un’analisi
attenta però mostra che nei punti P1 e P2 si è consumato moltissimo combustibile:
la velocità iniziale (rossa) e quella finale (blu) sono quasi perpendicolari.
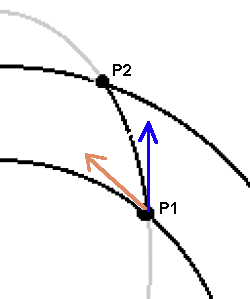 E’
E’
come frenare un TIR in corsa fino a farlo arrestare, e poi farlo ripartire
in direzione perpendicolare. Quanto più il vettore blu è parallelo al
vettore rosso, tanto più economico è il trasferimento di orbita.
Portando
la situazione all’estremo, se il vettore blu fosse proprio parallelo
al vettore rosso, allora una semplice accelerazione ci porterebbe sull’orbita
di trasferimento e una successiva accelerazione ci metterebbe in orbita
di destinazione. L’orbita di trasferimento più economica dunque è tangente
sia nel punto di partenza che nel punto di arrivo, ed è chiamata orbita
di Hohmann. Questo trasferimento è il più usato in campo astronautico,
perché è quello che consente il massimo risparmio il carburante. Tuttavia
non è il più veloce, per cui pianificando una missione spaziale si dovranno
valutare diversi fattori: ad esempio, dovendo sbarcare l’uomo su marte,
dovremo fare sì che il viaggio duri poco, e allo stesso tempo che il carburante
necessario sia il minimo.
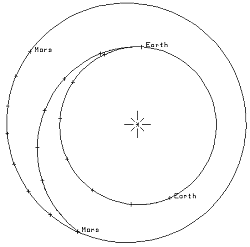 A
A
destra vediamo l’orbita che ha seguito la sonda Pathfinder
per giungere su Marte. I più attenti avranno notato che in prossimità
dell’arrivo su Marte le traiettorie non sono parallele! Infatti in questo
caso dobbiamo tenere conto della presenza del pianeta, e studiare una
particolare orbita che si chiama orbita di cattura.
Per tornare
al problema posto dalla domanda, l’orbita geostazionaria è un’orbita privilegiata
fra le infinite possibili, perché è caratterizzata da un periodo orbitale
di 24 ore esatte, dunque dalla superficie terrestre il satellite appare
fisso. Questo fa sì che si possano utilizzare parabole fisse per inviare
e ricevere dati dal satellite. Dalla seconda legge di Keplero e sapendo
che il periodo orbitale è di 24 ore, possiamo determinare
la distanza alla quale collocare il satellite perché sia geostazionario,
questa distanza risulta essere 35.920 km.
Normalmente
quando si lancia un satellite verso un’orbita geostazionaria si seguono
due fasi: il lancio con l’inserimento in un’orbita “di parcheggio” alla
quota di circa 1000 km, e il successivo trasferimento sull’orbita definitiva
utilizzando per il trasferimento proprio un’orbita di Hohmann.
Questa procedura è adottata per tutti i lanci: anche quelli interplanetari.
Il vantaggio del lancio in due fasi consiste nella possibilità di ridurre
gli errori. Se infatti il satellite venisse subito lanciato verso l’orbita
definitiva, un piccolo errore comporterebbe il dover correggere la traiettoria
quando il satellite è già lontano, manovra molto difficile!
 Per
Per
divertirsi imparando, consigliamo il programma Space simulator 1.0 della
Microsoft, che consente di simulare una grande quantità di missioni spaziali,
e sperimentare “sul campo” le leggi della navigazione spaziale.