Indicheremo con R il raggio del cilindro intorno a cui la corda si avvolge e con d il diametro della sezione trasversale della corda, infine con h l'altezza del cilindro. Vogliamo calcolare la lunghezza della curva individuata dalla spina della corda, cioè la curva descritta dai centri delle sezioni della corda, colorata di rosso in Fig. 1. Tale curva è detta elica cilindrica e si avvolge attorno ad un cilindro di raggio r = R + d/2. Se decidessimo di misurare la lunghezza della curva descritta dalla parte di corda che si appoggia al cilindro, la curva blu in Fig. 1, otterremo certamente una misura minore.
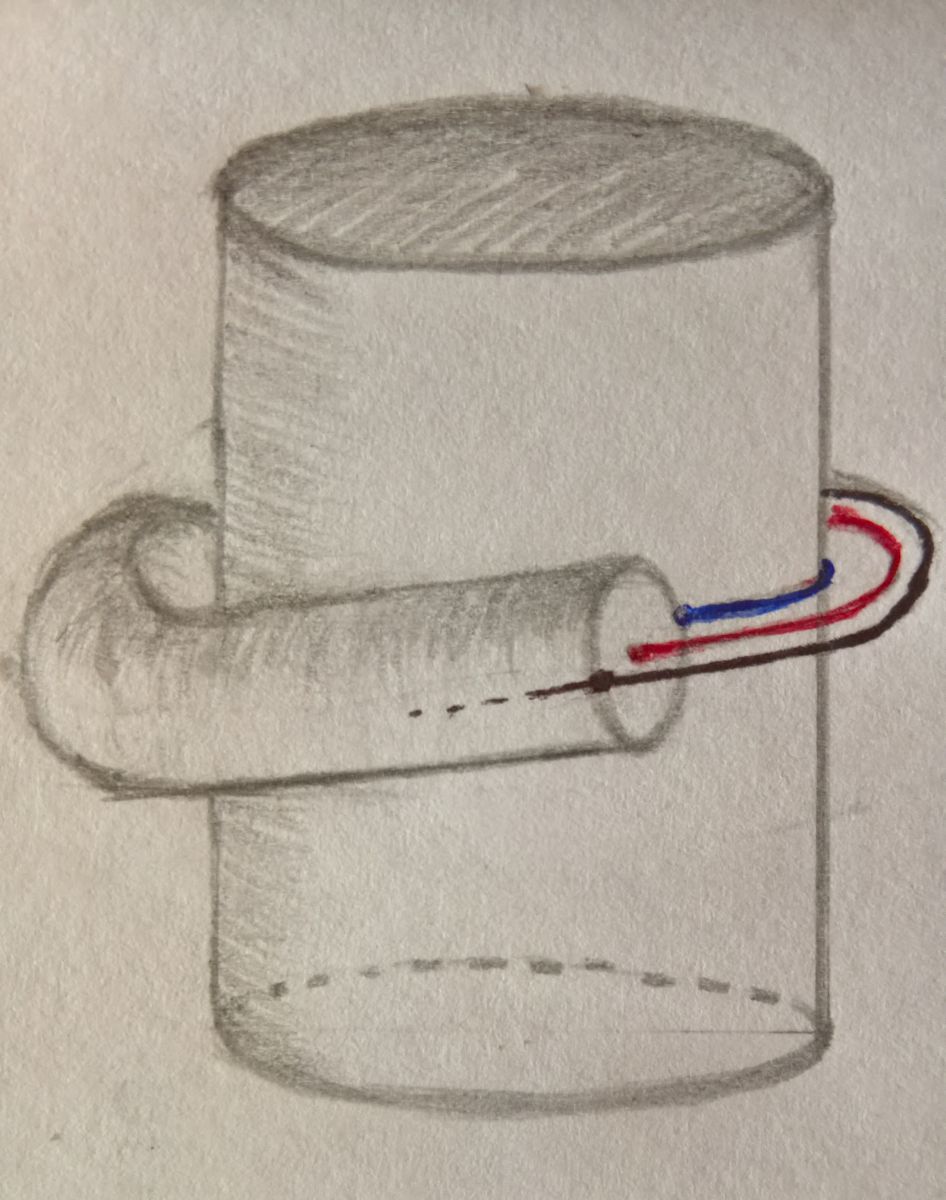
Fig. 1
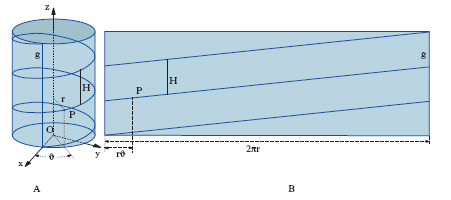
Srotoliamo su un piano il cilindro attorno a cui la spina della corda si avvolge, come illustrato in Fig. 2. Tale cilindro avrà altezza pari a g = h – d, poiché la spina della corda inizia ad avvolgersi d/2 più in alto della base del cilindro e finisce il suo percorso d/2 più in basso. Questa operazione non altera le lunghezze, approfondiremo meglio questo aspetto più avanti, e ci permetterà di risolvere il problema molto più agevolmente.
Fig. 2
Un avvolgimento dell'elica nella Fig. 2-A corrisponde ad un segmento in Fig. 2-B, che è l'ipotenusa di un triangolo rettangolo di cateti lunghi 2πr e H, dove H è il passo dell'elica, cioè la minima distanza tra due punti distinti dell'elica sulla stessa verticale. In Fig. 3 è riportato un ingrandimento del triangolo blu in Fig. 2-B, dove AB = 2πr, BK = d ed infine BC è il passo H dell'elica, che dobbiamo trovare. Essendo il triangolo ABC simile al triangolo BCK si ha BC:BK = AB:AK, che permette di trovare il passo dell'elica.
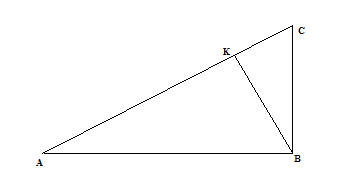
Fig. 3
Quindi, grazie al teorema di Pitagora, troviamo che la lunghezza di un avvolgimento è
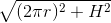 .
.
Per ottenere la lunghezza totale basta moltiplicare per il numero di avvolgimenti, che si ottiene dividendo l'altezza g per H.
Il quesito posto offre anche uno spunto per approfondire alcuni importanti aspetti geometrici. Ricordiamo che
Definizione 1: Una superficie è detta sviluppabile se è isometrica ad un piano, cioè può essere appiattita su un piano senza stiramenti o compressioni.
Il cilindro è una superficie sviluppabile, se la domanda richiedesse la lunghezza di una curva sulla sfera non si potrebbe procedere in modo simile poiché la sfera non è una superficie sviluppabile. Solitamente la definizione precedente viene così formulata:
Definizione 2: Si definisce sviluppabile una superficie con curvatura Gaussiana nulla in ogni punto.
La curvatura Gaussiana in un punto x di una superficie è il prodotto delle due curvature principali, che sono il massimo ed il minimo della curvatura di una curva passante per x e contenuta nella superficie (per la definizione di curvatura di una curva si veda http://www.vialattea.net/esperti/php/risposta.php?num=14596). I seguenti teoremi dimostrano l'equivalenza delle precedenti definizioni.
Teorema egregium: La curvatura Gaussiana è invariante per isometrie della superficie.
Teorema (di Minding): Se due superfici hanno curvatura Gaussiana uguale e costante allora sono isometriche.
Infine da questo esercizio emerge un'interessante proprietà dell'elica cilindrica. Una geodetica è una curva che descrive localmente la traiettoria più breve tra due punti su una superficie. Un arco di un'elica cilindrica è una geodetica: teniamo presente infatti che siamo passati dalla Fig. 2-A alla Fig. 2-B senza compressioni o stiramenti, ciò significa che la distanza tra due punti presi su una delle rette blu in Fig. 2-B rimane invariata quando la retta si arrotola sul cilindro per formare un tratto di elica.
Riferimenti:
http://www.treccani.it/enciclopedia/elica/
Approfondimenti:
Un commento
I commenti sono chiusi.