Caduta dei gravi, non nel vuoto. Rosa dice che il corpo più pesante atterra sempre prima. Carlo sostiene che i due corpi, se avessero stessa forma e dimensioni, ma peso diverso, cadrebbero alla stessa velocità: prendendo due sfere cave identiche e mettendo in una di esse un sasso e nell’altra nulla, esse atterrerebbero insieme. Chi ha ragione?

Su un corpo in caduta nell’aria agiscono tre forze: la forza di gravità, l’attrito viscoso con l’aria e la spinta di Archimede.(¹)

Per loro natura le forze di attrito hanno sempre direzione coincidente con la direzione del moto e verso opposto. Se il moto avviene lungo una linea retta (immaginiamo un corpo che cada da fermo) allora le tre forze saranno allineate, in quanto il moto avviene lungo una verticale. L’effetto combinato dell’attrito e della forza di galleggiamento sarà dunque quello di ‘rallentare’ la caduta rispetto allo stesso moto in  assenza di aria.

Infatti, la forza di gravità è proporzionale alla massa del corpo, e la spinta di Archimede fa sì che di fatto dobbiamo sottrarre dalla massa del corpo la massa dell’aria spostata.

La forza di attrito può essere invece considerata ragionevolmente proporzionale alla sezione e alla velocità ( o a qualche potenza della velocità, ma questa è un’altra storia…). Facendo l’ipotesi che l’attrito dell’aria sia descrivibile con una proporzionalità diretta rispetto alla velocità e alla sezione (cosiddetto moto laminare), possiamo scrivere l’equazione del moto proiettata su un asse verticale orientato dal basso verso l’alto:

$$ma=-(m-m_a)g+kSv$$

dove a è l’accelerazione del corpo, v la sua velocità, m la sua massa ed m_a la massa dell'aria spostata. S è la sezione e k una opportuna costante che dipende dalle caratteristiche viscose del fluido. Non entriamo nei complessi meccanismi della resistenza viscosa dell’aria; chi fosse interessato può approfondire partendo dalla pagina di Wikipedia:

https://it.wikipedia.org/wiki/Attrito#Attrito_viscoso

Poiché nella equazione del moto le quantità a e v dipendono dal tempo, essa rappresenta una equazione differenziale, in cui cioè compaiono delle grandezze e alcune loro derivate: cioè l'incognita è una variabile che dipende dalle sue stesse variazioni! Questa appena ricavata effettivamente rappresenta uno dei casi più semplici di equazioni differenziali.

Senza integrare esplicitamente l’equazione scritta, possiamo facilmente vedere che, se non ci fosse l’effetto dell’aria, tutti i corpi cadrebbero con la stessa accelerazione verso il basso (l’accelerazione di gravità),  quindi con la stessa velocità e impiegherebbero lo stesso tempo. Infatti nell’equazione del moto il termine di massa si semplificherebbe  e resterebbe a=-g. (²)

Consideriamo ora la presenza dell’aria, facendo comunque il caso di corpi ben più densi. L’acqua è circa 800 volte più densa dell’aria, e il legno più leggero circa 100 volte. In tal caso (m-m_a)/m è praticamente 1, e l’equazione si semplifica molto dividendo per m ambo i membri:

$$a=-g+kSv/m$$

 Il termine aggiuntivo di attrito, non dipendendo dalla massa, fa sì che il contributo dell’aria incida di più sui corpi più leggeri, cioè quelli con minore inerzia. Si vede infatti che l’ultimo termine ha un peso inversamente proporzionale alla massa. Se la massa è piccola incide molto, mentre se la massa è molto grande diviene trascurabile rispetto all’accelerazione. Ovviamente, più cresce la velocità più questo termine diventa importante, con il risultato che la forza netta di accelerazione verso il basso diminuisce. Ad un certo punto la velocità sarà tale che questo contributo bilancia esattamente la forza di gravità ed il corpo prosegue praticamente a velocità costante. Questo è il motivo per cui i paracadutisti riescono ad atterrare (quasi sempre) illesi: la loro velocità limite di caduta è diminuita dalla resistenza del paracadute e rimane costante finché toccano il suolo.

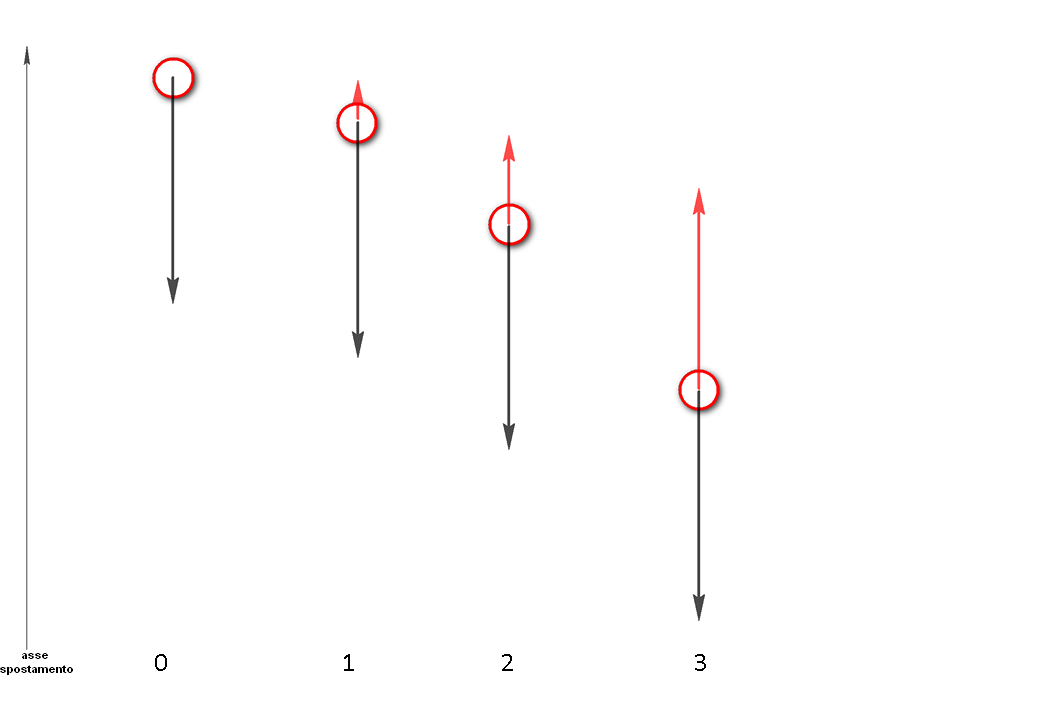
Figura 1.

All’inizio (tempo 0) il corpo subisce solo la risultante di forza di gravità e galleggiamento, essendo fermo. Subito dopo (tempo 1) gravità e galleggiamento restano gli stessi, mentre la velocità ormai, non nulla, introduce una componente ‘frenante’ sul corpo. Al tempo 2 questa componente cresce visto che la  velocità è aumentata, finché al tempo 3 la forza di attrito viscoso bilancia completamente la gravità e il corpo si muove con velocità uniforme, in quanto la risultante delle forze è nulla. Se il termine di attrito si annulla, non esiste più velocità limite e la velocità continua ad aumentare proporzionalmente al tempo!

 

Infine possiamo considerare il caso in cui il corpo sia poco più denso dell’aria: allora anche il termine di galleggiamento influisce sul moto, facendo sì che l’accelerazione di gravità sia efficacemente contrastata. L’accelerazione iniziale sarebbe allora:$$-g(m-m_a)$$Considerando comunque che, ad esempio, il polistirolo espanso ha densità superiori a 20 volte quella dell’aria, questa è una condizione difficile da osservare, per lo meno con corpi omogenei. Si può ad esempio immaginare meglio con un palloncino riempito a fiato, o meglio con una pompa (per diminuire la concentrazione di anidride carbonica, più densa dell’aria).

Quanto detto finora si può comunque verificare facilmente utilizzando due palline da ping pong: una vuota (comunque piena di aria!) e l’altra riempita di acqua con una siringa. Si constata immediatamente che la pallina piena giunge a terra prima di quella vuota, se vengono lasciate cadere dalla stessa altezza!

Un interessante video su questo argomento si può trovare qui:

http://video.mit.edu/watch/feather-and-coin-in-a-vacuum-6407/

In definitiva, se parliamo di due corpi esternamente identici il più pesante cade più in fretta, ma in condizioni diverse non è sempre vero. Un corpo molto grande e poco denso (pensiamo ad un palloncino di gomma riempito a fiato (peso dell’ordine di qualche g) e un punto metallico per la spillatrice (peso: un ventesimo di grammo) non arriveranno a terra insieme. In tal caso, infatti, i termini di galleggiamento e di attrito saranno così diversi da permettere velocità limite molto diverse, facendo sì che il punto metallico arrivi a terra prima del palloncino. Qundi non ha ragione nessuno dei due!

Una trattazione più dettagliata e matematicamente corretta è consultabile al seguente link:

http://webusers.fis.uniroma3.it/~ottica/sant/fis1/pdffiles/compl2.pdf

 

(¹) Dobbiamo infatti anche considerare le forze di pressione che agiscono sulla superficie del corpo, calcolabili con la legge di Stevino. Poiché la pressione dell’aria diminuisce con l’altezza, l’effetto netto di queste forze è che il corpo riceve una spinta verso l’alto pari al peso dell'aria che occuperebbe il suo stesso volume (fluido spostato), cosicché se la sua densità è minore della densità dell’aria si otterrebbe una forza netta che spinge il corpo verso l’alto (spinta di Archimede). Infatti, sia il corpo un cubetto di lato δh. La forza esercitata dalla pressione dell’aria (in equilibrio idrostatico) che agisce sulla parete superiore è dunque -ρgh, mentre sulla parete inferiore sarà +ρg(h-δh), ove ρ è la densità del fluido circostante. Sulle pareti laterali la pressione è la stessa, stando alla stessa altezza, e pertanto la forza risultante è nulla. L’effetto netto è quindi F = – ρ g S δh = m_a g, se si considera che ρV è per definizione uguale alla massa. Ciò fa sì che un corpo con densità minore dell’aria tenda a salire, mentre uno più pesante a cadere.

(²) Questo risultato, che a prima vista può sembrare banale, nasconde in realtà in sé uno dei principi cardine della fisica: l’equivalenza tra massa inerziale e massa gravitazionale. Da un lato, infatti, si era capito almeno dal tempo di Newton che una forza applicata ad un corpo ne produce un’accelerazione, e tale accelerazione è proporzionale alla forza tramite una costante detta massa (cioè, tanto più è massivo il corpo, tanto maggiore è la forza che devo imprimere per accelerarlo). D’altra parte, però, si capì anche che questa stessa ‘qualità’ implicava l’attrazione gravitazionale tra due corpi (cioè, un corpo più massivo è attratto maggiormente da un altro e risulta più pesante). Questo era un fatto curioso ed accettato come dato di fatto in fisica classica (ma non spiegabile), finché Einstein non ne fece un caposaldo per introdurre la relatività generale. Egli immaginò un ascensore con una persona chiusa all’interno: questa non sarà mai in grado di stabilire se si trovi in uno spazio privo di gravità oppure in caduta libera. Questa considerazione lo portò ad interpretare la gravità come una proprietà dello spazio-tempo e non come un campo. Ma qui il discorso si complica e diventa una storia a sé…