Salve, cosa significa che in R^4 ci sono infinite strutture differenziali?

Ecco il link alla mia video-introduzione: http://youtu.be/MPrUdXPf4Eg.

Per poter rispondere al meglio a questa domanda trovo utile ricordare alcune definizioni:

Definizione 1. Sia (M,T) uno spazio topologico di Hausdorff diciamo che una coppia 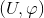 è una carta locale su M di dimensione n se U è un aperto in M e  è un omeomorfismo tra U e .  Inoltre se  è un'altra carta locale su M, diciamo che  e 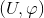 sono compatibili se  oppure, nel caso , se le applicazioni

sono funzioni di classe . 

Definizione 2. Sia (M,T) uno spazio topologico di Hausdorff e sia 

una famiglia di carte locali di dimensione n su M. Diciamo che A è un atlante di dimensione n su M se la famiglia  è un ricoprimento di M e se le carte  sono a due a due compatibili. 

Definizione 3. Diciamo che due atlanti A e A' sono equivalenti se  è un atlante su M e diciamo che A è massimale se non esiste un atlante A' su M equivalente ad A tale che . 

Definizione 4. Sia (M,T) uno spazio topologico di Hausdorff. Diciamo infine che M è una varietà differenziabile se su M è dato un atlante massimale di dimensione n, tale atlante è detto struttura differenziabile.

Definizione 5. Siano M e N due varietà differenziabili, sia A un aperto in M,   una funzione e sia . Diciamo che  è differenziabile in p se per ogni carta locale 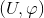 su M attorno a p e per ogni carta locale  su N attorno a , tali che , la mappa

è di classe  in . Se poi  è differenziabile in ogni  allora si dice che  è differenziabile. Diciamo poi che  è un diffeomorfismo se è biiettiva e  e  sono entrambe differenziabili. 

Affermare che in  ci sono infinite strutture differenziabili significa che esistono infiniti atlanti massimali su  che generano varietà differenziabili. È probabile che la domanda faccia riferimento a un fatto che invece è specifico per . Vale infatti un importante risultato:

Teorema: Per ogni  tutte le varietà differenziabili costruibili sullo spazio topologico euclideo di  sono tra loro diffeomorfe. Invece esiste un'infinità (precisamente con la stessa cardinalità del continuo) di varietà differenziabili costruibili sullo spazio topologico euclideo   tra loro non diffeomorfe.

Per chiarire le idee facciamo un esempio in  con topologia euclidea. Sia A l'atlante avente come carta locale l'applicazione identica e sia A' l'atlante avente come carta: 

per ogni U_j aperto. È evidente che A e A' non sono equivalenti, infatti 

non è . Per il teorema sopra citato possiamo concludere che (,A) e (,A') devono essere diffeomorfe. Si nota infatti che, scelta , le applicazioni

sono entrambe , e quindi  è un diffeomorfismo.  

Capita, invece,  che su  esistono strutture differenziabili non diffeomorfe. Vengono dette  esotici le varietà differenziabili su  non diffeomorfe a (,A), dove le carte locali in A sono applicazioni identiche. Equivalentemente si può affermare che un  esotico è una varietà differenziabile omeomorfa ma non diffeomorfa allo spazio euclideo .