L’orizzonte cosmico si trova alla distanza di 13,7 miliardi di anni luce. Si legge, però, che la sua distanza effettiva è di 47 miliardi di anni luce perché nel frattempo l’universo si è espanso. In base a quali calcoli si ottengono queste distanze? E’ concepibile un universo infinito in espansione? Grazie

Il concetto di distanza in cosmologia richiede sempre grande attenzione, per cui cerchiamo di chiarire a cosa corrispondono le quantità indicate nella domanda. Innanzitutto, non è completamente corretto dire che l’orizzonte cosmico si trova alla distanza di 13,7 miliardi di anni luce. È corretto dire che l’Universo ha un’età di 13,7 miliardi di anni. Un fotone emesso subito dopo il Big Bang ha viaggiato per 13,7 miliardi di anni, una quantità che viene denominata tempo di volo. Come dice il lettore, però, lo spazio nel frattempo si è espanso, per cui la distanza tra noi ed il punto di emissione è maggiore di 13,7 miliardi di anni luce.

Si definisce distanza propria tra due punti nell’Universo la distanza misurata con un ipotetico righello lunghissimo che connette i due punti (per esempio, due galassie). Perché questa misura abbia senso, è necessario che i due estremi del righello siano letti al medesimo istante t, il che risulta ai fini pratici impossibile in cosmologia. Quando osserviamo una galassia lontana, la vediamo infatti ad un tempo precedente al nostro, perché la sua luce ha impiegato un certo tempo a raggiungerci. Conoscerne la distanza all’istante attuale è possibile, ma non particolarmente utile. La distanza propria tra due punti, inoltre, cambia con l’espansione dell’Universo anche se questi due punti sono "a riposo", cioè senza che su di loro agisca alcuna forza esterna. Si ricorre pertanto al concetto di distanza comovente, una distanza che rimane invariata nel tempo per oggetti a riposo. In pratica, la definizione di distanza comovente include una correzione che tiene conto dell’espansione dell’Universo.

I due numeri indicati nella domanda sono dunque, rispettivamente, il cosiddetto tempo di volo della luce dall’origine dell’Universo ad oggi, e la distanza comovente dell’orizzonte. Il loro calcolo non è particolarmente complicato, ma necessita di una nutrita serie di premesse, in quanto l’Universo nel suo insieme viene descritto dalle non immediate leggi della Relatività Generale. Per ulteriori approfondimenti, si possono consultare i riferimenti riportati a fondo pagina. Cercando di limitarsi al minimo indispensabile, il primo concetto di base è che lo spazio-tempo ha una geometria non euclidea, e risulta uno spazio curvo. In condizioni di omogeneità ed isotropia, la metrica ha la forma seguente (detta di Robertson-Walker):

ds² = –c²dt² + a²(t)[dr²/(1-kr²) + r²dΩ²],

(1)

dove a è il fattore di scala (che dipende dal tempo t), k è una costante (legata alla curvatura dello spazio), c è la velocità della luce, r è la coordinata radiale, e dΩ è l’elemento di angolo solido. In quanto segue, consideriamo soltanto direzioni radiali per cui dΩ = 0. La funzione a(t) e la costante k dipendono dal contenuto dell’Universo (materia, energia, radiazione). Questi due parametri si possono determinare utilizzando le equazioni di Einstein, che legano la metrica al contenuto di massa energia dell’Universo. In questo caso, una delle equazioni di Einstein si può scrivere nel seguente modo (equazione di Friedmann):

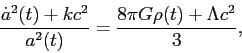(2)

dove compare esplicitamente la densità ρ della materia, mentre G è la costante gravitazionale, e Λ la cosiddetta costante cosmologica. Il punto denota la derivata rispetto al tempo. Si vede come ρ e Λ determinano l’evoluzione nel tempo del parametro a(t). Questo risulta intuitivo: un Universo con un’alta densità di materia avrà un’espansione più lenta rispetto ad un Universo a bassa densità. Per connettere questa equazione a quantità direttamente osservabili, si introducono delle variabili alternative. In primo luogo, al posto del fattore di scala, si utilizza il cosiddetto redshift z, definito da

1+z = a₀/a,

(3)

dove a₀ = a(t₀) è il valore del fattore di scala al tempo odierno t₀. Si può dimostrare che il redshift misura il rapporto tra la lunghezza d’onda osservata (o) ed emessa (e) di un raggio di luce (z = λ_o/λ_e-1), per cui risulta una quantità direttamente osservabile. Si definiscono anche le seguenti quantità:

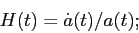ρ_c(t) = 3H²(t)/(8πG);
Ω_m = ρ(t₀)/ρ_c(t₀);
Ω_Λ = c²Λ/(3H₀²).

(4)

Il valore di H calcolato per t = t₀ si chiama costante di Hubble e viene indicato con H₀. La densità ρ_c viene chiamata densità critica, ed Ω_m ed Ω_Λ sono la densità della materia e dell’energia del vuoto, rispettivamente, normalizzate alla densità critica. Le costanti H₀, Ω_m ed Ω_Λ sono misurabili sperimentalmente attraverso diversi test cosmologici ed osservazioni astronomiche. Le loro determinazioni più recenti sono H₀ = 67.3±1.2 km s^-1 Mpc^-1, Ω_m = 0.315±0.017, Ω_Λ = 0.685±0.017. Si definisce infine Ω_k = –kc²/(a₀H₀²), e si può dimostrare che Ω_m + Ω_Λ + Ω_k = 1 (i valori misurati di Ω_m ed Ω_Λ implicano che Ω_k, e quindi k, sia uguale a 0 entro gli errori).

Dopo questa lunga serie di premesse, passiamo finalmente alla definizione e determinazione delle distanze. Usando l’espressione della metrica riportata sopra (1), e ricordando che la distanza propria D_p è la distanza misurata da due osservatori simultanei (dt = 0), si ha:

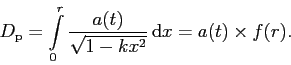(5)

Si vede esplicitamente che D_p dipende dal tempo in quanto è proporzionale ad a(t), mentre la funzione f dipende solo da r. La distanza comovente D_c è definita in modo da "adattarsi" all’espansione dell’universo, ed è:

D_c = (a₀/a)D_p = a₀ × f(r).

(6)

L’orizzonte è formato da quei punti che hanno emesso fotoni subito dopo il Big Bang (a = 0, o equivalentemente z → +∞). Per calcolare la distanza comovente con l’orizzonte, possiamo seguire il percorso di un fotone, per il quale ds² = 0, e quindi dall’espressione della metrica (1) si ricava la relazione:

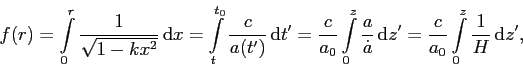(7)

dove abbiamo calcolato 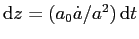differenziando la (3).

Possiamo ora usare l’equazione di Friedmann (2) per calcolare l’evoluzione del parametro a(t) in funzione del tempo, e quindi di H(t). Dobbiamo però conoscere l’evoluzione della densità in funzione del tempo. Senza addentrarci nella dimostrazione, risulta intuitivo che, limitandosi a materia "normale" (non relativistica), ρ(t) = ρ(t₀) (a₀/a)³ = ρ(t₀)(1+z)³, cioè la densità cresce avvicinandosi al Big Bang proporzionalmente all’inverso del volume. Abbiamo finalmente tutti gli elementi per calcolare D_c. Possiamo riscrivere l’equazione di Friedmann (2) cambiando la variabile da t a z, ricordando la definizione (3) di z, ed usando le quantità H₀, Ω_m, Ω_Λ, e Ω_k definite nella (4):

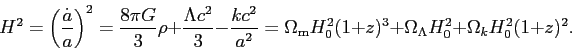(8)

Sostituendo il valore di H dalla (8) nella (7), e utilizzando la definizione (6), otteniamo il risultato finale:

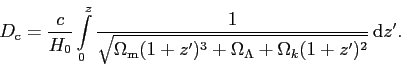(9)

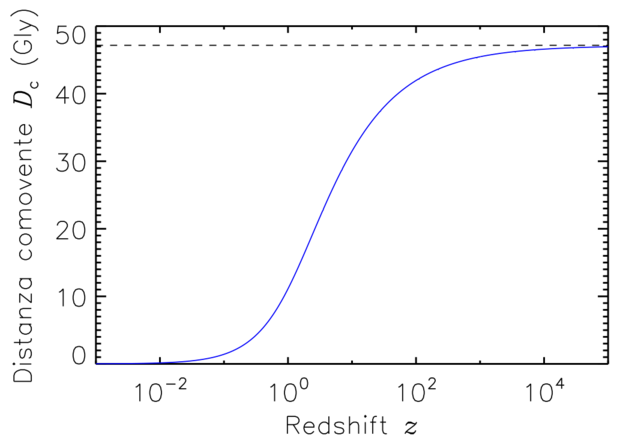
Questo integrale purtroppo non si può calcolare analiticamente. Per z → +∞, la funzione integranda è proporzionale a z^-3/2, per cui l’integrale converge ad un valore finito. Il risultato si può approssimare numericamente (al computer) usando i valori misurati di H₀, Ω_m, e Ω_Λ. L’andamento di D_c è mostrato nella figura. Si vede che per z → +∞, D_c ≈ 47 Gly (1 Gly = 1 miliardo di anni luce, dall’inglese light year).

La seconda quantità richiesta nella domanda è il tempo di volo di un fotone emesso all’orizzonte. Differenziando la definizione (3) di redshift, otteniamo:

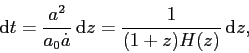(10)

ed utilizzando ancora la (8) troviamo:

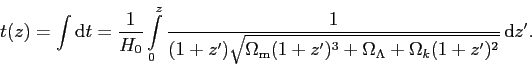(11)

Neppure questo integrale è calcolabile analiticamente, ma il suo valore numerico per z → +∞ risulta 13.8 miliardi di anni (la leggera discrepanza col valore indicato nella domanda può essere dovuta a differenti valori utilizzati per i parametri cosmologici).

Per quanto riguardo l’ultima parte della domanda, se sia concepibile un universo infinito in espansione, rimando a una mia precedente risposta sul sito di Vialattea.net.

Approfondimenti.

Per calcolare l’evoluzione del parametro a in funzione del tempo si è assunto che la densità di massa-energia sia interamente sotto forma di materia ordinaria (non relativistica), per cui ρ = ρ_m ∝ (1+z)³. Questo è corretto al giorno d’oggi, ma, andando via via a ritroso nel tempo, l’Universo era sempre più caldo, per cui inizialmente l’energia era dominata dalla componente radiativa (fotoni ed in generale particelle relativistiche, in moto con velocità prossime alla velocità della luce). Per questa componente, la densità evolve in funzione di z come ρ_r ∝ (1+z)⁴. Fin quando ρ_m > ρ_r, la descrizione riportata sopra è corretta, ma per z molto grandi l’effetto della radiazione diventa dominante. La transizione avviene al cosiddetto redshift di equivalenza, che si può calcolare z_eq = 5800. L’andamento della funzione integranda nelle equazioni (9) ed (11) cambia per z > z_eq. All’atto pratico, però, i valori numerici non cambiano di molto, in quanto la stragrande maggioranza della distanza comovente e del tempo di volo avviene nel regime dominato dalla materia (come si vede per esempio nella figura).
Per la precisione, l’orizzonte menzionato nella domanda si chiama orizzonte di particella, e corrisponde alla distanza che un raggio di luce ha viaggiato tra il Big Bang ed oggi. In cosmologia, esiste anche l’orizzonte degli eventi, che corrisponde alla massima distanza che un fotone può viaggiare tra oggi e la fine dei tempi (che può essere infinito).

Riferimenti bibliografici.

Riferimenti su Wikipedia: la metrica di Robertson-Walker, le equazioni di Friedmann, la distanza comovente.
D. Hogg, "Distance measures in cosmology", arXiv:astro-ph/9905116 (in inglese).
T. Davis e C. H. Lineweaver, "Expanding Confusion: common misconceptions of cosmological horizons and the superluminal expansion of the Universe", Publ. Astron. Soc. Australia, Vol. 21, pp. 97-109, disponibile a questo link (in inglese).
Planck collaboration: "Planck 2013 results. XVI. Cosmological parameters", arXiv:1303.5076 (in inglese).
F. Lucchin, "Introduzione alla cosmologia", ed. Zanichelli (ISBN: 9788808012432).