Vi sono vari metodi per eseguire le moltiplicazioni e le divisioni dei numeri binari. Il metodo concettualmente più semplice è quello delle addizioni ripetute per fare la moltiplicazione e delle sottrazioni ripetute per fare una divisione.
Per eseguire la moltiplicazione a·b basta fare la somma a+a+a+…+a per b volte, mentre per eseguire la divisione a/b si farà a-b-b…-b fino ad arrivare a zero: il numero di sottrazioni dà il quoziente.
Quindi per fare le moltiplicazioni e le divisioni è necessario saper fare le addizioni (le sottrazioni sono un caso particolare delle addizioni, e addirittura codificando i numeri in un formato particolare, cioè in complemento a 2, non vi è alcuna differenza tra le due operazioni). L’addizione di due numeri binari si fa come per quelli decimali: si mettono in colonna e si sommano le singole cifre:
an an-1 … a1 a0 +
bn bn-1 … b1 b0 =
… a0+b0
in decimale se la somma delle cifre raggiunge dieci si scrive l’ultima cifra e si riporta la decina sulla colonna successiva, analogamente per i binari se la somma raggiunge 2 (10)b si scrive 0 e si riporta 1 sulla colonna successiva:
an an-1 … a1 a0 +
bn bn-1 … b1 b0 +
cn cn-1 … c1 =
sn sn-1 … s1 s0
Il circuito che implementa questa operazione è abbastanza semplice e soprattutto è modulare, cioè può essere composto da un numero arbitrario di cellette elementari per poter fare addizioni di una lunghezza voluta.
L’operazione di addizione di due numeri ad un bit è uguale alla operazione di XOR (or esclusivo) che dà uno se uno solo degli ingressi è uno:
questa è la tabella della verità di questa operazione e a fianco è riportato il simbolo circuitale
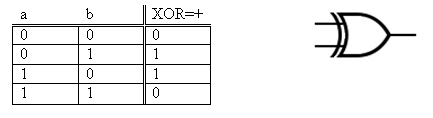
Per eseguire le operazioni su numeri a più bit bisogna considerare il riporto (carry in inglese): la celletta elementare che esegue la somma ad un bit con il riporto si chiama sommatore completo (full-adder)
.jpg)
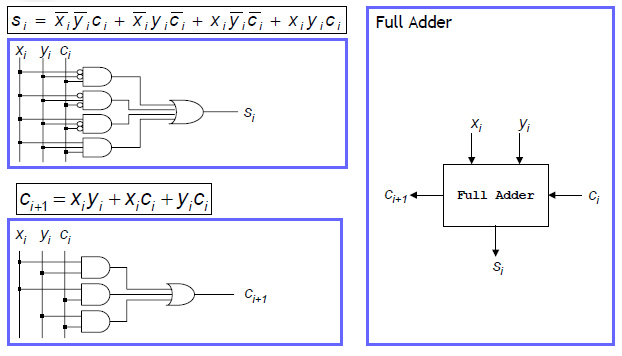
Per moltiplicare due numeri di n bit ciascuno occorre allora un sommatore completo a 2·n bit ed occorrono 2n-1 iterazioni (nel caso peggiore): per numeri di 32 bit sono 4 miliardi di iterazioni (!)
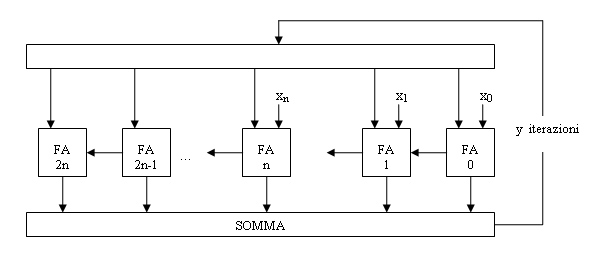
Il problema di questo approccio è l’elevato numero di operazioni. Si risparmiano molte operazioni facendo la moltiplicazione come per i numeri decimali, sommando i prodotti parziali del moltiplicando con le singole cifre del moltiplicatore:
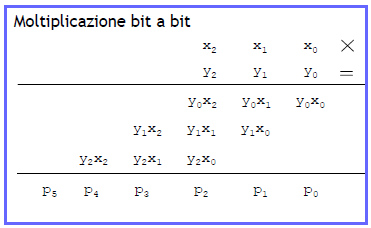
In questo caso il numero di moltiplicazioni e di addizioni è n2 cioè circa 1000 per numeri di 32 bit, inoltre n di esse vengono eseguite in parallelo tramite una rete combinatoria, quindi il risultato è quasi istantaneo, a parte il ritardo di transito nelle porte logiche.
I prodotti bit a bit sono effettuati tramite l’operazione AND, di cui è riportata la tabella di verità e il simbolo circuitale:
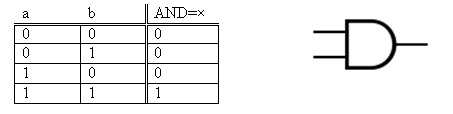
Le somme in colonna sono implementate con dei full adder.
Esistono anche altri algoritmi ancora più efficienti.
La divisione, oltre al metodo banale e impraticabile delle sottrazioni ripetute, può essere effettuata ancora con il metodo standard della divisione dei numeri decimali:

L’algoritmo si implementa con un’iterazione da 1 a n, due shift register e un sommatore a 2·n bit.