Semplicemente considerando le funzioni non periodiche come caratterizzate da un periodo infinito.
Si ricorda, per altri lettori, che è possibile sviluppare in una serie infinita di componenti sinusoidali aventi frequenza multipla intera (armoniche) le funzioni continue e periodiche. Sia s(t) un segnale di periodo T e f = 1/T, le ampiezze delle componenti armoniche sono date da:
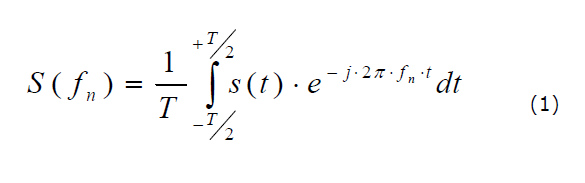
con fn = n f1 (fondamentale) e n intero compreso tra -∞ e +∞ .
Non tutte le funzioni s(t) periodiche e continue possono essere raffigurate da uno sviluppo in serie di Fourier, ma solo quelle che soddisfano le condizioni di Dirichlet: cioè se oltre che continue e periodiche hanno solo discontinuità di prima specie (limite destro e sinistro finiti ma diversi) oppure possono avere un numero finito di massimi e minimi che siano perfettamente integrabili. In soldoni che la funzione sia assolutamente e fisicamente realizzabile (es. un filtro analogico o numerico).
Ciò è in sintesi quello che si studia sui sacri testi. Per chi invece non ha avuto modo di “toccarle con mano” si immagini il vettore unitario e– j 2 π fn t come “un utilissimo attrezzo” che cerca e calcola ampiezze e frequenze sull’insieme di frequenze comprese tra -∞ e +∞, i componenti di vettori periodici su tutto il segnale s(t).
Infatti, se rappresentassimo anche il segnale s(t) con il formalismo esponenziale si osserverà che il prodotto con il vettore unitario che ruota in direzione opposta con velocità angolare – ω, fornirà un vettore fisso (riga spettrale) appena incontra una componente periodica (vettore rotante) di frequenza uguale o multipla intera di f1. Per tutte le altre componenti, invece, di frequenze diverse il prodotto fornirà ancora un vettore ma che ruota con frequenza differenza delle due frequenze e sul periodo l’integrazione fornirà un valore nullo.
Da qui, si afferma che un segnale continuo periodico nel dominio del tempo (visto all’oscilloscopio) risulta discreto e non periodico nel dominio della frequenza (visto all’analizzatore di spettro).
Detto in un altro modo, solo se le velocità angolari dei vettori sono multipli interi della velocità angolare del vettore fondamentale, tutte le componenti armoniche rotanti si trovano nella stessa posizione dopo ogni periodo T.
Quanto esposto, che si trova sotto forme diverse, per dire la stessa cosa, in decine di risposte su Vialattea ed altrove, è chiamato nello scenario dei segnali “analisi armonica”.
L’operazione inversa, cioè note le righe spettrali s(f), (misurate all’analizzatore di spettro, ricostruire il segnale s(t) funzione del tempo (che si vedrà all’oscilloscopio) prende il nome di “ricostruzione armonica”
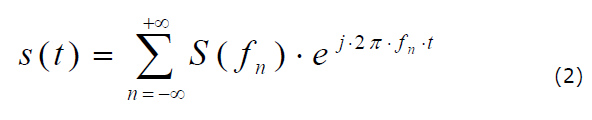
Da qui la potenza dell’operatore di Fourier (introdotto nel 1802 per descrivere, come somme di seni e coseni, funzioni molto complesse) che ci permette dal 1910 (Bell telephone) un rapido passaggio dei segnali tra i domini tempo – frequenza e viceversa.
La più familiare rappresentazione dei segnali è quella nel dominio del tempo (elettronici, informatici); vi sono molte situazioni in cui solo analizzando i segnali nel dominio della frequenza si riesce a rilevare degli aspetti non visibili nel dominio del tempo.
Tutte le considerazioni, non solo quelle esposte, sullo sviluppo in serie di Fourier, sono valide anche per funzioni non periodiche: come ho affermato all’inizio della risposta è sufficiente estendere l’integrazione sul periodo infinito.
Abbiamo detto che la distanza delle righe spettrali e pari a 1/T. Aumentando il periodo T le righe spettrali si avvicinano perché diminuisce la spaziatura. Facendo tendere T ad infinito la spaziatura delle righe tende a zero diventando uno spettro continuo ed il segnale s(t) perde la periodicità temporale.
Ecco il motivo per cui un segnale s(t) non periodico nel tempo ha una rappresentazione nel dominio della frequenza continua e non più discreta.
La relazione che trasforma una funzione s(t) non periodica dal dominio del tempo a quello della frequenza, non è altro che “l’analisi armonica” (1) con periodo infinito:
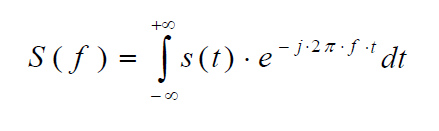
L’antitrasformata o trasformata inversa che trasforma una funzione dalla frequenza al tempo, è ricavata dalla “ricostruzione armonica” (2) ed è:
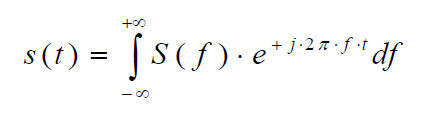
Penso che ora siano chiari i motivi per cui la serie di Fourier per i segnali periodici può considerarsi la funzione analoga alla “trasformata di Fourier” (e non trasformata inversa come è scritto nella domanda) per i segnali non periodici.