Quando la luce, o più in generale una qualsiasi radiazione elettromagnetica, si propaga non nel vuoto, si verifica una attenuazione dovuta essenzialmente a due cause: l’assorbimento e la diffusione. La rifrazione non è in causa direttamente, in quanto con questo termine ci si riferisce generalmente alla deviaizone della luce all’interfaccia tra due mezzi omogenei. In atmosfera, invece, non si ha mai a che fare con mezzi omogenei: nella migliore delle ipotesi, infatti, l’aria pulita è comunque una dispersione di molecole nel vuoto a grande distanze l’una dall’altra, e cio’ fa sì che le singole interazioni della radiazione con le molecole non possa essere descritta nei termini di ottica geometrica. A grande scala si può parlare di rifrazione, quando si consideri la variazione della densità dell’aria con la quota, la temperatura o l’umidità. Delle formule per calcolare l’indice di rifrazione atmosferico le ho scritte in questa precedente risposta.
In generale, comunque, in atmosfera sono disperse anche moltissime particelle molto più grandi delle molecole sia solide che liquide, dette comunemente pulviscolo, ma che tecnicamente sono indicate come aerosol.
Sono in realtà queste i principali ostacoli alla propagazione della luce in atmosfera, infatti gli astronomi, per questo e per altri motivi connessi alla turbolenza, preferiscono installare i telescopi in alta quota, dove la torbidità è minore e quindi le immagini sono più nitide.
RADIAZIONE IN UN MEZZO
Vediamo ora cosa succede alla radiazione che si propaga in un mezzo: ogni volta che un’onda piana (leggi un raggio) incontra una discontinuità nelle proprietà (schematizzabili per i nostri scopi tramite un numero, l’indice di rifrazione) elettriche e magnetiche del mezzo stesso, essa subisce una ‘ ridistribuzione’ che, dal punto di vista macroscopico, consta di assorbimento e diffusione. La somma di questi due termini viene detta estinzione, visto che entrambi contribuiscono a depauperare l’energia dalla direzione primitiva del fascio.
E’ da notare che la diffusione implica una rimozione di energia dal fascio ed una sua ridistribuzione angolare, che conserva il flusso di energia iniziale, mentre l’assorbimento implica una trasformazione in altre forme (principalmente termica).
La legge di Bouguer-Lambert-Beer stabilisce che l’intensità del fascio decresce esponenzialmente man mano che si avanza all’interno del materiale. Per descrivere questo fenomeno si utilizza l’indice di rifrazione complesso, in cui cioè la parte immaginaria dà una sorta di ‘lunghezza di penetrazione’ all’interno del materiale.
Si può dunque scrivere:
ove a è il coefficiente di estinzione del mezzo. Questo può essere generalizzato a dispersioni e mezzi disomogenei utilizzando coefficienti di estinzione macroscopici, ottenuti cioè come media su una porzione finita di spazio (es. qualche cm3 di aria).
Ad esempio, in atmosfera (al suolo), coefficienti di estinzione tipici sono dell’ordine di 0.1 (1) km^-1, il che significa che la radiazione si attenua di circa un terzo per ogni chilometro (100 m) attraversato. Si possono avere coefficienti molto più alti (mille volte di più dentro le nubi o nella nebbia fitta), così che dopo pochi metri la luce è quasi del tutto estinta, fino a valori molto più bassi (anche mille volte meno) in alta montagna oppure ai poli.
In generale è molto difficile calcolare il coefficiente di estinzione dalle caratteristiche dell’aerosol contenuto, ed ancora più difficile è la soluzione del problema inverso (che oltretutto non è unica): di fatto si misura direttamente l’attenuazione di un fascio (laser, ad esempio) in un percorso noto e da questo si risale al coefficiente di estinzione.
Va detto, però, che il conto può essere fatto esattamente per alcuni tipi di particelle disperse in aria:
1) per particelle piccolissime (molecole), esiste la teoria di Rayleigh che ci permette di calcolare il coefficiente di estinzione in un’atmosfera (pulita) a pressione p e temperatura T, per una radiazione di lunghezza d’onda lambda:
il che per l’atmosfera standard (p=1013 hPa e T=288 K) ci dà alfa= 0.013 km-1, per una radiazione monocromatica verde a 532nm.
In un ambiente urbano come Roma, ad esempio, il coefficiente di estinzione al suolo dovuto agli aerosol è mediamente 0.2 km^-1, il che ci fa capire che queste particelle contribuiscono molto più delle molecole d’aria all’estinzione della luce in atmosfera.
2) per particelle sferiche Mie trovò una soluzione analitica agli inizi del secolo scorso: tale soluzione prevede esattamente la ridistribuzione di un’onda piana che incida su una sfera di dielettrico omogenea con indice di rifrazione complesso noto. Tale soluzione è la base di molte approssimazioni che tutt’oggi si utilizzano nell’ottica atmosferica. Per la complessità dei calcoli non entrerò nel dettaglio della trattazione; osservo solamente che si usa quando la taglia delle particelle che si considerano è confrontabile con la lunghezza d’onda (cioè dell’ordine del decimillesimo di millimetro o maggiore); tali particelle sono considerate ‘grandi’, in contrapposizione alle molecole e alle particelle più piccole presenti in atmosfera, dette nuclei di condensazione.
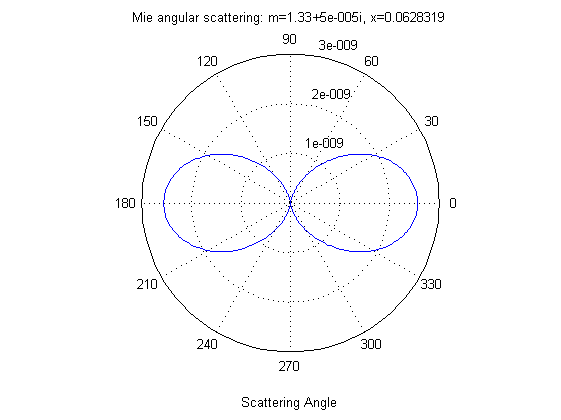
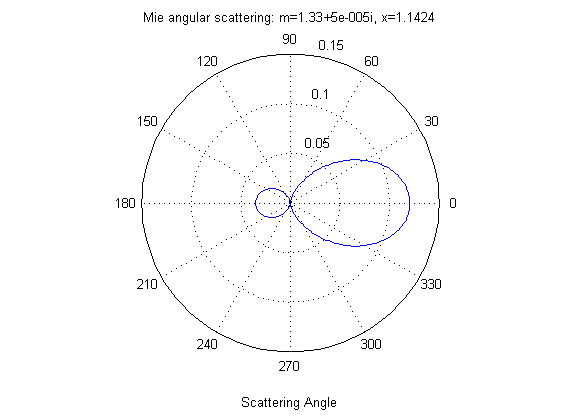
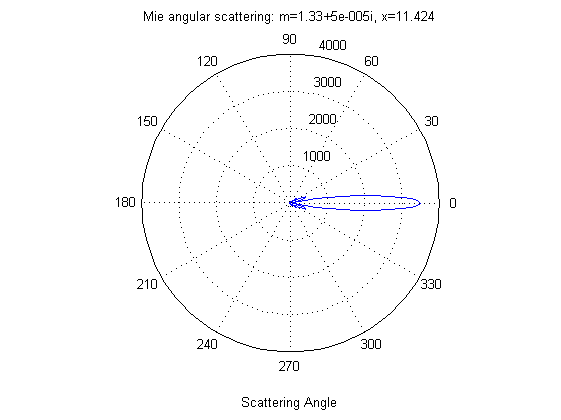
Le immagini riportano il diagramma angolare di diffusione di Mie per gocce d’acqua di raggi rispettivamente pari a .055, .1 ed 1 micron, per luce verde di 0.55 micron. E’ evidente il diverso comportamento al variare della grandezza della particella. Nel primo caso si ha praticamente una diffusione alla Rayleigh (simmetrica in avanti e all’indietro), mentre man mano che la particella cresce si osserva un aumento della diffusione ‘in avanti’ e a piccoli angoli.
CALO DI CONTRASTO E VISIBILITA’
Nel discorso precedente ho discusso l’attenuazione di un fascio luminoso che si propaga in atmosfera. In realtà la nitidezza della visione dipende dalla diffusione in maniera più complessa, in quanto la diffusione laterale di luce a piccoli angoli ‘mescola’ per così dire dettagli vicini tra loro, degradando la visione che si percepisce in lontananza. Ciò si condensa comunemente nell’espressione ‘c’è foschia’. Tecnicamente ciò si definisce come un calo di contrasto, dovuto appunto alla diffusione laterale delle particelle ‘grandi’. Va comunque osservato che tale fenomeno è a grandi linee proporzionale all’estinzione, per cui ci si aspetta che per grandi estinzioni si abbia anche un forte calo di contrasto e viceversa. Il discorso fatto in precedenza resta quindi valido in generale.
RUOLO DELL’ACQUA
A questo punto è doveroso accennare al ruolo dell’acqua in questo meccanismo. L’umidità libera non influenza direttamente la visibilità, ma si può depositare sulla superficie degli aerosol, accrescendone le dimensioni e alterandone l’indice di rifrazione, e ciò avviene praticamente sempre, in quanto in bassa atmosfera c’è generalmente molta acqua disponibile (dell’ordine dei grammi a metro cubo).
Tutto ciò comporta una variazione delle proprietà ottiche, in genere abbastanza difficile da prevedere. Accenno solo al fatto che ciò che conta nell’accrescimento è quasi esclusivamente l’umidità relativa, per cui sono state trovate varie formule empiriche che descrivono abbastanza bene il comportamento ottico di una particella immersa in aria umida.
Uno dei più utilizzati è il modello di Kasten (1968), che prevede un andamento del tipo:
ove gamma è un parametro empirico che adatta meglio la curva alle evidenze sperimentali. A causa della sua natura empirica, però, questa rappresentazione necessita di un archivio di parametri adatti ad ogni situazione sperimentale e difficilmente calcolabili a priori. Per contro, il vantaggio di questo approccio è che si può applicare a molte quantità ( ad esempio l’estinzione), misurando opportunamente l’esponente.
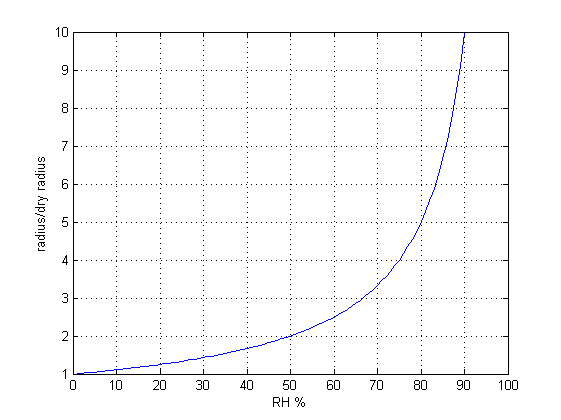
Grafico dell’aumento di raggio o di estinzione per una particella in equilibrio in aria con diversa umidità relativa. Il modello presenta una divergenza fittizia per RH=100%, cosa che in realtà non si verifica.
Il modello termodinamico di Kohler, elaborato negli anni ’30, permette invece un conto esatto dell’accrescimento di una goccia, una volta nota l’umidità relativa e la specie chimica della particella secca, ma è troppo complesso per essere trattato qui. A questo si può poi accoppiare il modello di Mie per avere una stima della diffusione della luce in diverse condizioni di umidità. Ovviamente il problema è alquanto complesso ed è tuttora oggetto di studio.
STAGIONALITA’
Ciò detto, è evidente che le migliori condizioni di visibilità si hanno quando c’è poco aerosol e l’umidità è bassa. Ciò, per lo meno in Italia, si verifica per lo più in condizioni di avvezione di aria da nord ( vento di Tramontana), che apporta aria secca e pulita dalle regioni settentrionali. Tali masse d’aria risultano in genere pulite dalle precipitazioni sul versante nord delle Alpi, e pertanto è facile avere visibilità di 100 km ed oltre ( ad esempio dai Castelli romani si vedono i monti Cimini, e dal Gran Sasso si può vedere sia Roma che l’Adriatico). Viceversa, quando dominano avvezioni da sud (in particolare apporto di avvezione sahariana) la visibilità scende spesso al di sotto dei 20 km pur in condizioni di cielo sereno e bassa umidità relativa.
Le stagioni, quindi, entrano in gioco solamente per la predominanza dei regimi di circolazione (da nord in inverno, da sud in estate) e per la variazione di temperatura, che determina una maggiore o minore umidità relativa a parità di umidità assoluta.