La domanda è probabilmente suggerita dal fatto che,
oltre alla ovvia soluzione a = b, questa equazione ha
almeno un’altra soluzione “famosa”: infatti,
24 = 16 =42. È allora lecito
chiedersi se esistano altre coppie di numeri che si comportano in questo modo
e, nel caso, se sia possibile determinarle analiticamente.
È possibile
rendersi conto (ragionando sulle proprietà di base delle potenze) che
se l’equazione è soddisfatta a e b devono avere lo
stesso segno; ragionando allo stesso modo è anche possibile capire che
se a e b sono negativi l’unica soluzione di questa equazione
è quella banale, cioè a = b.
Restringiamoci dunque al caso in cui a e b sono positivi: in
questo modo, siano ben definite le funzioni esponenziali aventi questi due
numeri come base.
Dal momento che a
e b sono positivi esiste un numero reale
x = loga(b) tale che
b = ax. L’equazione diventa allora
a(a^x) = aax, che
è soddisfatta se e solo se ax = ax, se e
solo se ax – 1 = x.
È facile allora rendersi conto che per ogni valore di a tale
equazione ammette sempre la soluzione x = 1 (che
corrisponde a a = b). Inoltre, se a è
maggiore di 1 e diversa da e = 2.71828… esiste anche un’altra
soluzione x1: se 1 < a < e
si ha x1 > 1, mentre se
a > e si ha
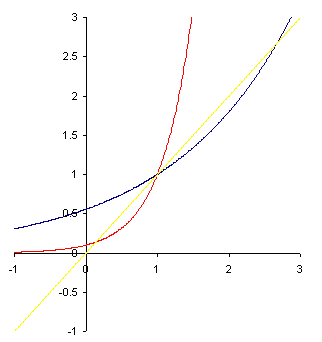
0 < x1 < 1: ad esempio si veda la
figura sottostante, dove sono rappresentate le tre curve di equazione
y = x (in giallo),
y = 1.8x – 1 (in blu) e
y = 10x – 1 (in rosso). Si noti
quindi che, dal momento che b = ax1,
se la coppia a, b è una soluzione non banale dell’equazione
ab = ba, allora b è
maggiore o minore di a a seconda che a sia maggiore o minore di e.
Insomma, ci sono buone notizie e cattive notizie. La buona
notizia è che, sebbene la risposta possa forse essere in parte
sorprendente, esistono infinite soluzioni non banali dell’equazione
ab = ba. La cattiva notizia
è che tali soluzioni dipendono l’una dall’altra tramite un’equazione
trascendente, cioè non possono essere determinate per via algebrica.
Per determinarle è necessario approssimarle secondo i metodi del calcolo
numerico.