L’interno del Sole è dotato di densità e temperature molto elevate. Solo in queste condizioni, infatti, sono possibili le reazioni nucleari che permettono il sostentamento della nostra stella. I fotoni di alta energia rilasciati da queste reazioni, dunque, finiscono inevitabilmente per interagire (urtare) contro le particelle circostanti (nuclei ed elettroni), che a loro volta riemettono rapidamente nuovi fotoni. In questo senso, dunque, nessun fotone emesso all’interno del Sole raggiunge la superficie. Questa catena di scambi, però, è in stato di equilibrio, per cui per ogni fotone assorbito ne viene rapidamente emesso uno nuovo. Gradualmente, dunque, l’energia prodotta al centro del Sole viene trasportata verso gli strati esterni. Alla fine, i fotoni raggiungono una regione della sfera solare dove la densità è sufficientemente bassa per cui possono finalmente sfuggire nello spazio circostante. Sono questi i fotoni che osserviamo a Terra, e la regione dove il Sole diventa trasparente è detta fotosfera.
L’intero processo di fuga è molto lungo, e infatti richiede migliaia di anni. Se per incanto all’interno del Sole le reazioni nucleari si interrompessero di colpo, noi per molto tempo continueremmo a beneficiare dell’energia prodotta dal Sole mentre questa si propaga dal centro fino alla superficie.
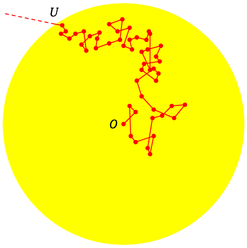 Come già detto, i fotoni vengono continuamente distrutti e ricreati. Per visualizzare il processo, possiamo pensare ad una specie di staffetta, in cui ad ogni interazione un fotone passa il "testimone" al successivo e si ferma. Il percorso seguito da questa ipotetica squadra di atleti risulterebbe alquanto bizzarro, in quanto non seguirebbe una linea retta, e nemmeno una direzione privilegiata, variando in modo casuale dopo ogni interazione. È per questo che il tempo necessario ad uscire è così lungo. La figura a fianco rappresenta un esempio di questo tipo di percorso, dove un fotone è emesso nel punto O e si guadagna faticosamente la strada, interazione dopo interazione, fino ad uscire nel punto U. Si tenga presente che nel disegno si sono segnate circa una cinquantina di deviazioni, ma in realtà il loro numero è enormemente maggiore (circa 5×1021). Il processo è stato qui rappresentato in due dimensioni, mentre nella realtà avviene naturalmente in tre; la trattazione è però perfettamente analoga nei due casi.
Come già detto, i fotoni vengono continuamente distrutti e ricreati. Per visualizzare il processo, possiamo pensare ad una specie di staffetta, in cui ad ogni interazione un fotone passa il "testimone" al successivo e si ferma. Il percorso seguito da questa ipotetica squadra di atleti risulterebbe alquanto bizzarro, in quanto non seguirebbe una linea retta, e nemmeno una direzione privilegiata, variando in modo casuale dopo ogni interazione. È per questo che il tempo necessario ad uscire è così lungo. La figura a fianco rappresenta un esempio di questo tipo di percorso, dove un fotone è emesso nel punto O e si guadagna faticosamente la strada, interazione dopo interazione, fino ad uscire nel punto U. Si tenga presente che nel disegno si sono segnate circa una cinquantina di deviazioni, ma in realtà il loro numero è enormemente maggiore (circa 5×1021). Il processo è stato qui rappresentato in due dimensioni, mentre nella realtà avviene naturalmente in tre; la trattazione è però perfettamente analoga nei due casi.
Vediamo di fornire una stima, approssimata ma quantitativa, del tempo di uscita. È necessario introdurre il concetto di libero cammino medio λ, che è la distanza media percorsa da un fotone tra quando è stato emesso e quando viene riassorbito. Questa quantità dipende naturalmente dalle condizioni fisiche del mezzo in cui è immerso (in particolare dalla sua densità), ma come cruda approssimazione possiamo assumere che λ si mantenga costante all’interno di tutto il Sole. Numericamente, λ vale circa 1 cm.
Siano li = (xi, yi) gli spostamenti (vettoriali) percorsi dopo ogni interazione. Dopo N urti, la posizione del fotone sarà data dalla somma vettoriale degli spostamenti:
L = Σi li,
dove il simbolo Σ indica la somma. La distanza dal centro L = |L| si trova applicando più volte il teorema di Pitagora:
L2 = Σi xi2 + Σi yi2 + 2(x1x2 + y1y2 + x1x3 + y1y3 + …),
dove xi ed yi sono le coordinate di ogni punto[1]. Nell’equazione sopra, il termine tra parentesi contiene innumerevoli addendi (tutte le possibili coppie xixj ed yiyj con i < j). Ognuno di questi addendi può essere tanto positivo che negativo, mentre in media i valori di xi ed yi rimangono simili. Dopo molti urti, dunque, la somma tra parentesi tenderà ad annullarsi, mentre i due termini quadratici rimangono sempre positivi. Per N grande, dunque, si può approssimare:
L2 ≈ Σi (xi2 + yi2) = Σi |li|2.
Assumendo che, in media, |li| ≈ λ (per definizione di libero cammino medio), troviamo finalmente il risultato:
L = λ N1/2.
Si vede che la distanza dal centro aumenta col numero di urti, ma solo come la radice quadrata di N. Al contrario, la distanza totale percorsa dal fotone è D = Σi li ≈ Nλ, che è un fattore N1/2 volte maggiore di L.
Il fotone arriverà alla superficie del Sole potendo finalmente fuggire quando L ≈ R, dove R è il raggio del Sole (circa 700000 km). Questo permette di determinare il numero di interazioni necessarie a raggiungere la superficie:
N ≈ (R/λ)2.
La distanza totale percorsa sarà dunque D = Nλ ≈ R2/λ. Se c è la velocità della luce, il tempo τ impiegato dai fotoni a percorrere questa distanza è infine dato da:
τ = D/c ≈ R2/(cλ),
che è il risultato cercato. Inserendo i valori numerici per R, c, e λ, si trova τ ≈ 5200 anni.
Nel considerare questo valore, bisogna sempre tenere a mente le approssimazioni effettuate. In primo luogo, il libero cammino medio dei fotoni nel Sole non è costante all’interno del suo volume, ma chiaramente diventa più piccolo nelle regioni centrali più dense. Il tempo di fuga sarà quindi in realtà più grande del numero riportato sopra, dato che vicino al nucleo i fotoni subiranno piu interazioni di quelle calcolate sopra. Inoltre, una frazione del Sole è percorsa da moti convettivi, dove cioè i fotoni non si propagano lungo un cammino casuale, ma intere regioni di materiale vengono trasportate collettivamente verso la superficie. In queste regioni, la trattazione sopra esposta non è valida.
Chiarimento. Come ricordato sopra, il cammino libero medio varia all’interno della sfera solare. In particolare, si ha λ = 1/(κρ), dove ρ è la densità e κ un coefficiente detto opacità (che pure dipende dalle proprietà del mezzo e dal tipo di interazione fotone/materia considerata). Il valore λ ≈ 1 cm riportato sopra assume per la densità il valore medio su tutto il Sole. In realtà, la densità non è costante, ma diminuisce via via che ci si avvicina alla superficie. In particolare, alla fotosfera il suo valore è circa 10 milioni di volte inferiore alla media. Per questo motivo, alla superficie, il libero cammino medio risulta, proporzionalmente, 10 milioni di volte superiore. La regione della fotosfera, dove viene emessa la radiazione solare, non è dunque spessa solo 1 cm, ma all’incirca 300 km. Di fatto, lo spessore d della fotosfera è definito proprio dalla relazione d = λ.
[1]Nota. Nel caso tridimensionale, la notazione è più involuta ma il risultato finale rimane identico: τ ≈ R2/(cλ). Lo spostamento dopo N urti sarà sempre L = Σi li, dove adesso li = (xi, yi, zi). Analogamente, la distanza dall’origine sarà data da:
L2 = Σi xi2 + Σi yi2 + Σi zi2 + 2(x1x2 + y1y2 + z1z2 + x1x3 + y1y3 + z1z3 + …).
Esattamente come nel caso bidimensionale, il termine tra parentesi diventa trascurabile per N grande, da cui L2 ≈ Σi (xi2 + yi2 + zi2) = Σi |li|2. Il calcolo riprende quindi come descritto sopra.