Per spostamento della linea degli apsidi si intende uno rotazione nel piano dell’orbita della linea che unisce afelio e perielio: la conseguenza è che l’orbita non è più un’ellisse chiusa ma assume la caratteristica forma “a rosetta”:
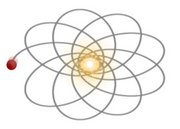
Durante questo moto ovviamente cambia la posizione del perielio, per questo ci si riferisce allo spostamento della linea degli apsidi anche come ad una “precessione del perielio”.
Questo movimento non riguarda solo Mercurio, ma anche gli altri pianeti del Sistema Solare. Per la Terra ad esempio la linea degli apsidi compie un giro completo in circa 117.000 anni, con una velocità angolare media di 11 secondi d’arco all’anno: di questo movimento (al contrario della rotazione o della rivoluzione) non ne percepiamo direttamente gli effetti, ma insieme con altri cosiddetti moti millenari può essere rilevante su grandi scale di tempo. Se sei interessato leggiti queste risposte (sul legame “spostamento linea degli apsidi-precessione degli equinozi” e sui loro possibili effetti sui cambiamenti climatici e sulle glaciazioni):
http://www.vialattea.net/esperti/php/risposta.php?num=6383
http://www.vialattea.net/esperti/php/risposta.php?num=11873
La teoria newtoniana della gravitazione, basata sulla legge:
per cui due masse si attraggono reciprocamente con una forza direttamente proporzionale al prodotto della masse e inversamente al quadrato della distanza, può rendere conto di questo tipo di moto. Se considerassi il moto di ciascun pianeta indipendentemente dal moto di tutti gli altri (cioè come se gli altri pianeti non ci fossero), la forza newtoniana pianeta-sole farebbe muovere il pianeta su un’orbita ellittica chiusa (prima legge di Keplero).
In realtà gli altri pianeti ci sono, ed anche loro attraggono il mio pianeta (sebbene in misura molto minore rispetto al Sole, per via della massa del Sole molto più grande rispetto alle altre). Se rendo il mio modello più realistico, considerando come si dice “perturbativamente” (cioè considerandola molto piccola, e quindi come una perturbazione) l’attrazione degli altri pianeti, ottengo che l’effetto è proprio una precessione del perielio.
Il problema è che la previsione newtoniana per Mercurio non coincide con il valore osservato di 574 secondi d’arco al secolo. Come calcolato da Le Verrier prima e da Newcomb poi (intorno alla metà dell’800) le perturbazioni newtoniane prevedono 43 secondi d’arco al secolo in meno. Per rendere conto di tutti i 574 secondi d’arco furono considerate varie ipotesi, tra cui quella della presenza di altri “pianeti” o corpi celesti tra Mercurio e il sole, ma nessuna di queste si rivelò valida e coerente con le osservazioni.
Solo la teoria della relatività generale di Einstein riuscì a prevedere esattamente quell’eccesso di 43 secondi d’arco al secolo rispetto alla teoria newtoniana, tanto che questa previsione insieme con quella sulla deflessione dei raggi luminosi in prossimità del sole e con il red-shift, è considerata uno dei test classici della teoria.
La relatività generale è una teoria in cui si scrivono le leggi che regolano i fenomeni fisici (fenomeni meccanici, elettromagnetici, onde, etc…) in modo tale che la forma di queste leggi o equazioni rimanga la stessa anche per un altro osservatore, che rispetto a quello di partenza, si muova ad esempio di moto uniforme, o accelerato, o rotatorio; in altre parole qualunque osservatore spiega i fenomeni fisici con le stesse leggi, da cui il termine relatività generale (in termini “tecnici” si dice che le leggi della fisica sono covarianti sotto una generica trasformazioni di coordinate). Questa richiesta di covarianza per le leggi della fisica “si paga” col fatto che osservatori diversi hanno metriche diverse, ovvero modi diversi di misurare le distanze. Qui entra in gioco la gravità: un osservatore che vede agire la forza di gravità, è in realtà un osservatore con una metrica curva, e la gravità è una conseguenza di questa curvatura della metrica e quindi dello spazio-tempo (i corpi sembrano attrarsi, ma in realtà sono indotti ad avvicinarsi dallo spazio-tempo curvato); ma esiste sempre (localmente) un altro osservatore con una metrica piatta, per il quale quindi non agisce nessuna forza di gravità; in questo senso nella relatività generale la gravità è una sorta di forza “apparente” cioè legata al particolare osservatore. Ciò che determina la metrica di un certo osservatore, e quindi la curvatura dello spazio-tempo grazie alla quale le masse sembrano attrarsi, sono le masse stesse o più in generale la distribuzione di energia-impulso.
Le equazioni di Einstein permettono, una volta nota questa distribuzione di energia-impulso, di ricavare la metrica e quindi la curvatura ( a patto di saper risolvere le equazioni, cosa tutt’altro che banale, perché sono equazioni differenziali “non lineari”):
![]() è il tensore energia-impulso, quello che dà la distribuzione di materia-energia;
è il tensore energia-impulso, quello che dà la distribuzione di materia-energia; ![]() è la metrica;
è la metrica; ![]() ed R sono rispettivamente il tensore di Ricci e la curvatura scalare che esprimono appunto la curvatura e sono legati alla metrica; GN è la costante di gravitazione universale, la stessa che compare nella legge di Newton ( c è la velocità della luce).
ed R sono rispettivamente il tensore di Ricci e la curvatura scalare che esprimono appunto la curvatura e sono legati alla metrica; GN è la costante di gravitazione universale, la stessa che compare nella legge di Newton ( c è la velocità della luce).
Se approssimiamo il sole come una massa sferica le equazioni si risolvono e forniscono la metrica e quindi la curvatura dello spazio-tempo da esso prodotta (soluzione di Schwarzschild); uno degli effetti di questa curvatura è proprio la precessione del perielio dei pianeti che gli orbitano intorno.
Il contributo relativistico alla precessione (chiaramente continuano ad esserci anche gli altri effetti “newtoniani” che spiegano gran parte del valore osservato) è dato da uno spostamento angolare del perielio:
Dove e è l’eccentricità dell’orbita ed a è il suo semiasse maggiore.
Come si vede la correzione relativistica è maggiore, quando il semiasse dell’orbita è minore; per questo la correzione è rilevante per Mercurio, che è il più vicino al sole. Se lo si calcola per Mercurio si ottengono proprio quei 43 secondi d’arco al secolo mancanti!