Lo scarto quadratico medio -SQM- (e la sua radice quadrata) di un insieme di valori è il più usato ed importante indice di dispersione statistica. La radice quadrata dello SQM è detta deviazione standard o deviazione quadratica media. In inglese si trova la notazione ‘RMS (root mean square) deviation’.
Indici di tendenza centrale e di dispersione
Supponendo di avere una collezione di misure (dette realizzazioni) di una certa variabile, è abbastanza comune fornire il valore medio definito mediante la media aritmetica dei valori misurati. La media aritmetica è solo uno degli indici di tendenza centrale di una distribuzione di dati; altri sono la mediana, la moda e le medie armonica e quadratica. La media aritmetica è però l’indice più usato, in quanto gode di alcune importanti proprietà. Nel seguito ci riferiremo esclusivamente alla media aritmetica.
Meno comune è, purtroppo, fornire una stima della variabilità delle misure, o più precisamente della dispersione attorno al valor medio: la media infatti non dà nessuna informazione su quanto i vari valori siano vicini tra loro: in altre parole, conoscere la dispersione è importante per sapere se la media è rappresentativa dell’insieme o meno.
Consideriamo infatti i due gruppi di campioni:
12 7 13 8 e:
4 18 2 16,
essi hanno entrambi media pari a 10, ma è evidente che il primo campione è molto più ‘concentrato’ attorno al valor medio, mentre il secondo è più ‘disperso’.
Per dare un’indicazione di questa proprietà si possono utilizzare diversi indicatori, il più comune dei quali è appunto lo SQM (e la sua radice), definito come la media aritmetica dei quadrati delle differenze tra ogni valore e la media (scarti). Il quadrato è usato perché ovviamente la media degli scarti è nulla, per definizione di media aritmetica.
Lo SQM è dunque, per un insieme di N valori:
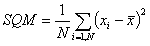 (1).
(1).
Nell’esempio citato, lo SQM vale 6.5 per il primo campione e 50 per il secondo. E’ allora chiaro come esso un ottimo candidato ad esprimere la dispersione delle misure attorno al valor medio.
E’ da notare che lo SQM può essere definito a partire da una media qualunque e non necessariamente dalla media aritmetica; è tuttavia dimostrabile che in tal caso esso assume il valore minore. E’ inoltre facile dimostrare che lo SQM può anche essere calcolato nel modo seguente:
SQM= <x2>-<x>2 (2),
ove con < > si è indicata l’operazione di media.
Spesso si calcola lo SQM dividendo per N-1 anziché per N come dato nella definizione precedente; questo perché si può dimostrare che il miglior stimatore della varianza di una distribuzione di valori è proprio la quantità
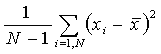 (3).
(3).
Più precisamente, in statistica si dimostra che, data una variabile casuale X, si ha:
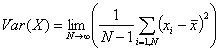 (4).
(4).
E’ evidente che per campioni molto grandi la differenza tra le due definizioni è trascurabile.
Nelle scienze applicate spesso si utilizza la deviazione standard di una serie di misure della stessa grandezza come errore casuale associato al valore medio. E’ opportuno ricordare come in campo scientifico non ha pressoché senso fornire una misura senza l’errore associato. Troppo spesso le statistiche riportano solo i valori medi, senza tenere conto che omettere la variabilità è nascondere gran parte dell’informazione!
Altri indici di dispersione
E’ naturalmente possibile utilizzare altri parametri per indicare la dispersione dei dati attorno al valore centrale, anche se, come detto, la grandezza più utlizzata è la deviazione standard.
In alcuni casi, però, si utilizzano altri indicatori:
La semidispersione massima è il più semplice indice di dispersione ed indica semplicemente la semidifferenza tra il valore massimo e minimo della distribuzione:
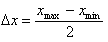 (5).
(5).
Poiché esso considera solo i valori estremi è estremamente sensibile alla presenza di punti molto ‘dispersi’ (outliers).
Se la distribuzione dei valori è fortemente asimmetrica lo SQM non è particolarmente interessante perché sottostima da un lato e sovrastima dall’altro la effettiva variabilità. Si possono allora utilizzare i percentili (cioè la percentuale di dati oltre il valore fissato: cioè il 70° percentile indica il valore oltre il quale sono presenti il 30% dei dati, ad esempio). Molto usati sono il 25° ed il 75° percentile. Il 50° percentile rappresenta il valore centrale (mediana) della distribuzione una volta ordinati i valori in ordine crescente ed è spesso usato al posto della media, in quanto pesa molto meno gli outliers.
Lo scostamento medio assoluto è dato invece dalla seguente quantità:
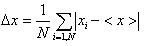 (6),
(6),
ove con <x> si è indicata una qualsiasi stima di tendenza centrale. E’ simile allo scarto quadratico medio, ma utilizza il modulo anziché il quadrato per ‘raddrizzare’ gli errori. Si può dimostrare che questa quantità è minima se si utilizza per <x> la mediana.
![]() (1).
(1).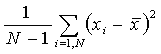 (3).
(3).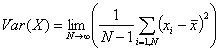 (4).
(4).![]() (5).
(5).![]() (6),
(6),