Il fattoriale di
un numero naturale n è dato dal prodotto di tutti i numeri naturali
minori di n. Per convenzione, il fattoriale di zero è pari a 1.
Ad esempio, il
fattoriale di 5 è pari a 5x4x3x2 = 120.
L’espressione
cercata dal lettore è la seguente funzione di variabile naturale a valori
naturali f:N®N
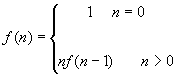
La funzione f
così definita è detta ricorsiva perché definita in termini di se stessa; una
espressione iterativa analoga della funzione f è la seguente:
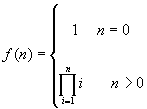
Applichiamo
l’espressione della funzione ricorsiva restituisce il prodotto dei numeri
naturali calcolando il fattoriale di 5:
f(5) = 5 f(4) = 5(4 f(3)) = 5(4(3 f(2))) = 5(4(3(2 f(1)))) = 5(4(3(2(1 f(0))))) =
5(4(3(2(1(1))))) = 120
La funzione
ricorsiva si espande in termini di se stessa per tutti i valori maggiori di
zero e nel valore 1 in zero.
L’espressione
iterativa fa invece uso della funzione “produttoria” che, nel caso n=5,
si legge come segue:
![]() = 1 2 3 4 5 = 120
= 1 2 3 4 5 = 120